
【题目】如图,已知某船于上午8时在A处观测小岛C在北偏东60°方向上,该船以每小时20海里的速度向东航行到B处,测得小岛C在北偏东30°方向上,船以原来的速度继续向东航行2小时,到达岛C正南方点D处,船从A到D一共航行了多少海里?

【答案】船从A到D一共走了120海里.
【解析】
根据直角三角形 30°角所对的直角边等于斜边的一半求出 BC 的长度,再根据两个方位角证明 AB=BC,根据AD=AB+BD即可求解.
由题意知∠CAD=30°,∠CBD=60°,
在△BCD 中,∠CBD=60°,
∴∠BCD=30°,
∴BC=2BD,
∵船从B到D走了2小时,船速为每小时20海里,
∴BD=40 海里,
∴BC=80海里,
由∠CBD=60°,得∠ABC=120°,
∵∠CAD=30°,
∴∠ACB=30°,
∴AB=BC,
∴AB=80海里,
∵AD=AB+BD,
∴AD=80+40=120(海里).
因此船从A到D一共走了120海里.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:
【题目】由于被墨水污染,一道几何题仅能见到如图所示的图形和文字:“如图,已知:四边形ABCD中,AD∥BC,∠D=67°,…”

(1)根据以上信息,你可以求出∠A、∠B、∠C中的哪个角?写出求解的过程;
(2)若要求出其它的角,请你添上一个适当的条件: ,并写出解题过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D,E分别在AB,AC上,要使DE∥BC,必须具备哪些条件?尽可能把所有条件写出来。

比如:
(1)如果∠DEC+∠ECB=180°,那么DE∥BC:
(2)_________________________________;
(3)_________________________________;
(4)_________________________________;
(5)__________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列定义一种关于n的运算:①当n是奇数时,结果为3n+5 ②n为偶数时结果是![]() (其中k是使
(其中k是使![]() 是奇数的正整数),并且运算重复进行.例如:取n=26,则…,若n=449,则第449次运算结果是( )
是奇数的正整数),并且运算重复进行.例如:取n=26,则…,若n=449,则第449次运算结果是( )
A. 1 B. 2 C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+3的图象分别交x轴、y轴于点B、点C,与反比例函数y= ![]() 的图象在第四象限的相交于点P,并且PA⊥y轴于点A,已知A (0,﹣6),且S△CAP=18.
的图象在第四象限的相交于点P,并且PA⊥y轴于点A,已知A (0,﹣6),且S△CAP=18. 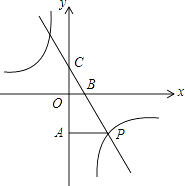
(1)求上述一次函数与反比例函数的表达式;
(2)设Q是一次函数y=kx+3图象上的一点,且满足△OCQ的面积是△BCO面积的2倍,求出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=1cm,BC=2cm,点P从点A出发,以1cm/s的速度沿折线AC→CB→BA运动,最终回到点A,设点P的运动时间为x(s),线段AP的长度为y(cm),则能够反映y与x之间函数关系的图象大致是( )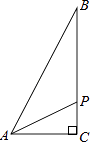
A.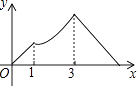
B.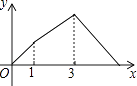
C.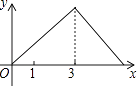
D.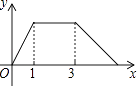
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,当点D的对应点D′落在∠ABC的角平分线上时,DE的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元. ①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台,若商店保持同种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com