
【题目】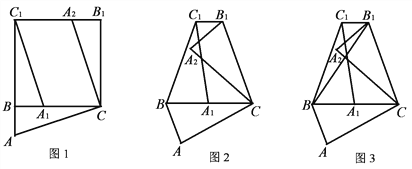
(1)如图1,在Rt△ABC中,∠ABC=90°,以点B为中心,把△ABC逆时针旋转90°,得到△A1BC1;再以点C为中心,把△ABC顺时针旋转90°,得到△A2B1C,连接C1B1,则C1B1与BC的位置关系为_______;
(2)如图2,当△ABC是锐角三角形,∠ABC=α(α≠60°)时,将△ABC按照(1)中的方式旋转α,连接C1B1,探究C1B1与BC的位置关系,写出你的探究结论,并加以证明;
(3)如图3,在图2的基础上,连接B1B,若C1B1=![]() BC,△C1BB1的面积为4,则△B1BC的面积为 .
BC,△C1BB1的面积为4,则△B1BC的面积为 .
【答案】(1)平行.(2)详解解析;(3)10
【解析】试题分析:(1)由旋转的性质可得∠C1BC=∠B1BC=90°,BC1=BC=CB1,根据平行线的判定方法可得BC1∥CB1,根据平行线的判定即可判定四边形BCB1C1是平行四边形,由平行四边形的性质即可得到结论;(2)C1B1∥BC,过C1作C1E∥B1C,交BC于E,由平行线的性质可得∠C1EB=∠B1CB,再由旋转的性质可得BC1=BC=B1C,∠C1BC=∠B1CB,即可得∠C1BC=∠C1EB,由等腰三角形的性质可得C1B=C1E,所以C1E=B1C,即可判定四边形C1ECB1是平行四边形,由平行四边形的性质即可得到结论;(3)已知C1B1∥BC,可得C1B1与BC 之间的距离相等,设这个距离为h,则△C1BB1的面积为![]() C1B1×h,△B1BC的面积为
C1B1×h,△B1BC的面积为![]() CB×h,又因C1B1=
CB×h,又因C1B1=![]() BC,△C1BB1的面积为4,即可得△B1BC的面积为10.
BC,△C1BB1的面积为4,即可得△B1BC的面积为10.
试题解析:
(1)平行.
(2)C1B1∥BC;
证明:过C1作C1E∥B1C,交BC于E,则∠C1EB=∠B1CB,
由旋转的性质知,BC1=BC=B1C,∠C1BC=∠B1CB,
∴∠C1BC=∠C1EB,
∴C1B=C1E,
∴C1E=B1C,
∴四边形C1ECB1是平行四边形,
∴C1B1∥BC;
(3)答案为:10.


科目:初中数学 来源: 题型:
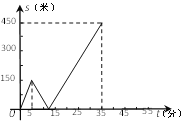
【题目】甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距![]() (米),甲行走的时间为
(米),甲行走的时间为![]() (分),
(分),![]() 关于
关于![]() 的函数函数图像的一部分如图所示.
的函数函数图像的一部分如图所示.
(1)求甲行走的速度;
(2)在坐标系中,补画![]() 关于
关于![]() 函数图象的其余部分;
函数图象的其余部分;
(3)问甲、乙两人何时相距360米?
查看答案和解析>>
科目:初中数学 来源: 题型:
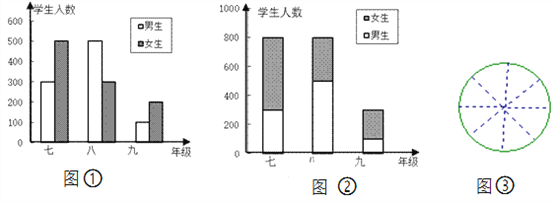
【题目】图①、图②是李晓同学根据所在学校三个年级男女生人数画出的两幅条形图.
(1)两个图中哪个能更好地反映学校每个年级学生的总人数?哪个图能更好地比较每个年级男女生的人数?
(2)请按该校各年级学生人数在图③中画出扇形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“日啖荔枝三百颗,不辞长作岭南人”,广东的夏季盛产荔枝,桂味、糯米糍是荔枝的品种之一.佳佳同学先用52元购买2千克桂味和1千克糯米糍;几天后,他用76元购买1千克桂味和3千克糯米糍.(前后两次两种荔枝的售价不变)
(1)求桂味、糯米糍的售价分别是每千克多少元?
(2)若佳佳同学用y元买了这两种荔枝共中10千克,设买了x千克桂味. ①写出y与x的函数关系式.
②若要求糯米糍的重量不少于桂味重量的3倍,请帮佳佳同学设计一个购买方案,使所需的费用最少,并求出最少费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳今年4月份某星期的最高气温如下(单位℃):26,25,27,28,27,25,25,则这个星期的最高气温的众数和中位数分别是( )
A.25,26B.25,26.5C.27,26D.25,28
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)若⊙O的直径为18,cosB=![]() ,求DE的长.
,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了丰富学生的体育活动,决定根据学生的兴趣爱好采购一批体育用品供学生课后锻炼使用,学校随机抽取了部分同学调查他们的兴趣爱好,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题: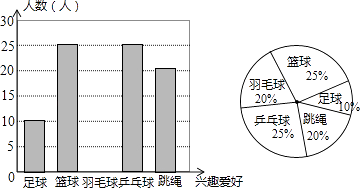
(1)设学校这次调查共抽取了n名学生,n= ;
(2)请你补全条形统计图;
(3)设该校共有学生1200名,请你估计该校有多少名学生喜欢跳绳?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com