
分析 因为将抛物线沿x轴翻折,所以得到的新抛物线和原抛物线关于x轴对称,进而可求出新抛物线的解析式,再根据抛物线平移的性质即可求出当t=0和t=2时抛物线C2的解析式.
解答 解:∵抛物线C1:y=$\frac{5}{9}$(x+2)2-5,
∴将抛物线沿x轴翻折后的抛物线解析式为-y=$\frac{5}{9}$(x+2)2-5,
即y=-$\frac{5}{9}$(x+2)2+5,
∴当t=0时抛物线C2的解析式为:y=-$\frac{5}{9}$(x+2)2+5,
当t=2时抛物线C2的解析式为:y=-$\frac{5}{9}$x2+5.
点评 本题考查了二次函数图象与几何变换,此类题目利用定点的变换确定解析式的变化更简便,难点在于确定出平移后的抛物线的顶点坐标.


科目:初中数学 来源: 题型:填空题
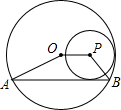 如图,⊙P内切于⊙O,⊙O的弦AB与⊙P相切,且AB∥OP,若⊙O的半径为3,⊙P的半径为1,则四边形ABPO的面积为2$+2\sqrt{2}$.
如图,⊙P内切于⊙O,⊙O的弦AB与⊙P相切,且AB∥OP,若⊙O的半径为3,⊙P的半径为1,则四边形ABPO的面积为2$+2\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
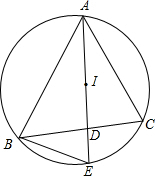 如图,点I是△ABC的内心,AI的延长线交边BC于点D,交△ABC外接圆于点E.
如图,点I是△ABC的内心,AI的延长线交边BC于点D,交△ABC外接圆于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| n | 8 | 0.008 | 0.000008 | 8000 | 8000000 | … |
| $\root{3}{n}$ | 2 | 0.2 | 0.02 | 20 | 200 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
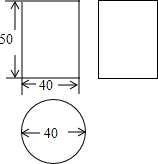 某工厂接受了加工100件密封罐的任务,设计者给出了密封罐的三视图(如图所示,单位:cm),已知加工这种密封罐需全部用铁皮焊接,那么该工厂至少要准备多少平方米的铁皮?
某工厂接受了加工100件密封罐的任务,设计者给出了密封罐的三视图(如图所示,单位:cm),已知加工这种密封罐需全部用铁皮焊接,那么该工厂至少要准备多少平方米的铁皮?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com