
| n | 8 | 0.008 | 0.000008 | 8000 | 8000000 | … |
| $\root{3}{n}$ | 2 | 0.2 | 0.02 | 20 | 200 | … |
科目:初中数学 来源:2017届云南省普洱市九年级学业水平测试模拟考试(一)数学试卷(解析版) 题型:单选题
我区5月份某一周的最高气温统计如下表:
最高气温( | 25 | 26 | 27 | 28 |
天 数 | 1 | 1 | 2 | 3 |
则这周最高气温的中位数与众数分别是( )
A. 27,28 B. 27.5,28 C. 28,27 D. 26.5,27
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
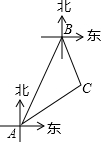 如图,点A、B是两个相距4000米的海岸观察点,点B位于点A的北偏东30°方向上,某日两观察点同时收到海面上的船C发出的信号,此时测得船C位于点A的北偏东60°方向上,位于点B的南偏东15°方向上,求此时船C到海岸AB的距离.(参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果精确到0.1米)
如图,点A、B是两个相距4000米的海岸观察点,点B位于点A的北偏东30°方向上,某日两观察点同时收到海面上的船C发出的信号,此时测得船C位于点A的北偏东60°方向上,位于点B的南偏东15°方向上,求此时船C到海岸AB的距离.(参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
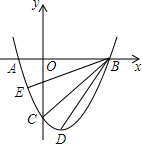 如图,抛物线y=ax2-2ax+b与x轴交于A、B两点,交y轴负半轴于点C,已知B(3,0),C(0,-3),D为顶点.
如图,抛物线y=ax2-2ax+b与x轴交于A、B两点,交y轴负半轴于点C,已知B(3,0),C(0,-3),D为顶点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com