
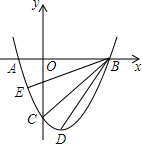
 如图,抛物线y=ax2-2ax+b与x轴交于A、B两点,交y轴负半轴于点C,已知B(3,0),C(0,-3),D为顶点.
如图,抛物线y=ax2-2ax+b与x轴交于A、B两点,交y轴负半轴于点C,已知B(3,0),C(0,-3),D为顶点.分析 (1)利用待定系数法即可求得抛物线的解析式;
(2)首先求得A、B和D的坐标,然后利用待定系数法求得BC的解析式,然后利用平移的性质求得D的对称点的坐标,从而求得直线BE的解析式,进而求得E的坐标.
解答 解:(1)根据题意得:$\left\{\begin{array}{l}{9a-6a+b=0}\\{b=-3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=-3}\end{array}\right.$,
则抛物线的解析式是y=x2-2x-3;
(2)y=x2-2x-3=(x-1)2-4,
则D的坐标是(1,-4).
在y=x2-2x-3中令x=0,解得y=-3,则C的坐标是(0,-3).
在y=x2-2x-3中令y=0,则x2-2x-3=0,解得x=-1或3,
则A的坐标是(-1,0),B的坐标是(3,0).
设直线BC的解析式是y=kx+b,
根据题意得:$\left\{\begin{array}{l}{3k+b=0}\\{b=-3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=-3}\end{array}\right.$,
则直线BC的解析式是y=x-3.
设过D且与BC垂直的直线解析式是y=-x+c,把(1,-4)代入得-1+c=-4,解得c=-3,
则直线的解析式是y=-x-3.则DE一定经过点C.
把D(1,-4)平移到C(0,-3)是向左平移一个单位长度,向上平移1个单位长度.
则把C向左平移一个单位长度,向上平移1个单位长度后得到D的对称点D',则D'的坐标是(-1,-2).
设直线BD'的解析式是y=mx+n,
根据题意得:$\left\{\begin{array}{l}{3m+n=0}\\{-m+n=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=\frac{1}{2}}\\{n=-\frac{3}{2}}\end{array}\right.$,
则直线BD'的解析式是y=$\frac{1}{2}$x-$\frac{3}{2}$.
根据题意得:x2-2x-3=$\frac{1}{2}$x-$\frac{3}{2}$,
解得:x=-$\frac{1}{2}$或3.
当x=-$\frac{1}{2}$时,y=$\frac{1}{2}$×(-$\frac{1}{2}$)-$\frac{3}{2}$=-$\frac{7}{4}$,则E的坐标是(-$\frac{1}{2}$,-$\frac{7}{4}$).
点评 本题考查了待定系数法求函数的解析式以及图象的平移、直线垂直的条件,正确求得D的对称点的坐标是关键.


科目:初中数学 来源:2017届山东省日照市莒县第三协作区九年级3月学业水平模拟考试数学试卷(解析版) 题型:解答题
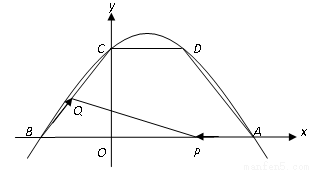
如图,抛物线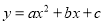 经过点A(5,0),B(-3,0),C(0,4).
经过点A(5,0),B(-3,0),C(0,4).
(1)求这条抛物线的函数关系式;
(2)过C作CD∥x轴交抛物线于D, 连续BC、AD,两个动点P、Q分别从A、B两点同时出发,都以每秒1个单位长度的速度运动.其中,点P沿着线段AB向B点运动,点Q沿着折线B→C→D的路线向D点运动.设这两个动点运动的时间为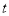 (秒)(0<
(秒)(0<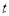 <7),△PQB的面积记为S.
<7),△PQB的面积记为S.
①求S与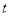 的函数关系式;
的函数关系式;
②当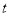 为何值时,S有最大值,最大值是多少?
为何值时,S有最大值,最大值是多少?
③是否存在这样的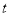 值,使得△PQB是直角三角形?若存在,请直接写出
值,使得△PQB是直角三角形?若存在,请直接写出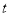 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| n | 8 | 0.008 | 0.000008 | 8000 | 8000000 | … |
| $\root{3}{n}$ | 2 | 0.2 | 0.02 | 20 | 200 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
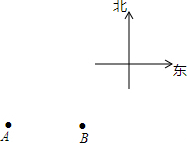 如图,A点和B点表示地面上的两个观测点,从A点观测到它的北偏东30°方向有一个读书亭C,同时,从B点观测到这个读书亭C在它的北偏西45°方向,试在图中确定读书亭C的位置.
如图,A点和B点表示地面上的两个观测点,从A点观测到它的北偏东30°方向有一个读书亭C,同时,从B点观测到这个读书亭C在它的北偏西45°方向,试在图中确定读书亭C的位置.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
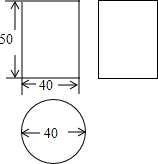 某工厂接受了加工100件密封罐的任务,设计者给出了密封罐的三视图(如图所示,单位:cm),已知加工这种密封罐需全部用铁皮焊接,那么该工厂至少要准备多少平方米的铁皮?
某工厂接受了加工100件密封罐的任务,设计者给出了密封罐的三视图(如图所示,单位:cm),已知加工这种密封罐需全部用铁皮焊接,那么该工厂至少要准备多少平方米的铁皮?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
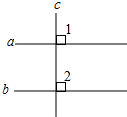 如图,已知a∥b,如果c⊥a,判断c与b的位置关系,并说明理由.
如图,已知a∥b,如果c⊥a,判断c与b的位置关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com