
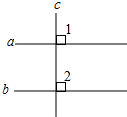
 如图,已知a∥b,如果c⊥a,判断c与b的位置关系,并说明理由.
如图,已知a∥b,如果c⊥a,判断c与b的位置关系,并说明理由. 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
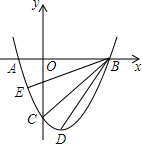 如图,抛物线y=ax2-2ax+b与x轴交于A、B两点,交y轴负半轴于点C,已知B(3,0),C(0,-3),D为顶点.
如图,抛物线y=ax2-2ax+b与x轴交于A、B两点,交y轴负半轴于点C,已知B(3,0),C(0,-3),D为顶点.查看答案和解析>>
科目:初中数学 来源:2017届山东省日照市莒县第三协作区九年级3月学业水平模拟考试数学试卷(解析版) 题型:单选题
如果关于x的一元二次方程kx2﹣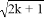 x+1=0有两个不相等的实数根,那么k的取值范围是( )
x+1=0有两个不相等的实数根,那么k的取值范围是( )
A. k< B. k<
B. k< 且k≠0 C. ﹣
且k≠0 C. ﹣ ≤k<
≤k< D. ﹣
D. ﹣ ≤k<
≤k< 且k≠0
且k≠0
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com