
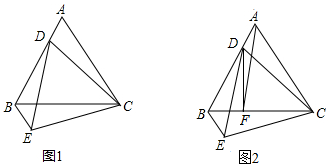
分析 (1)根据等边三角形的性质得到AC=BC,DC=EC,∠ACB=∠DCE=60°,推出△ACD≌△BCE,根据求三角形的性质得到AD=BE;
(2)根据平行线的性质得到∠BAF=∠BDE,推出∠BAF=∠BDE=∠ACD=∠BCE,证得△ABF≌△CBE,由全等三角形的性质得到BF=BE解直角三角形即可得到结论.
解答 (1)证明:∵△ABC,△CDE是等边三角形,
∴AC=BC,DC=EC,∠ACB=∠DCE=60°,
∴∠ACD=60°-∠BCD=∠BCE,
在△ACD与△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{DC=EC}\end{array}\right.$,
∴△ACD≌△BCE,
∴AD=BE;
(2)解:∵AF∥DE,
∴∠BAF=∠BDE,
∵∠BDC=∠BDE+CDE=∠BDE+60°=∠BAC+∠ACD,
∴∠BAF=∠BDE=∠ACD=∠BCE,
在△ABF与△CBE中,
$\left\{\begin{array}{l}{∠BAF=∠BCE}\\{AB=BC}\\{∠ABF=∠CBE}\end{array}\right.$,
∴△ABF≌△CBE,
∴BF=BE,
∵DF⊥BC,∠ABC=60°,
∴AD=BE=BF=BD•cos∠ABC=$\frac{1}{2}$BD,
∵AB=BC,AD=BF,
∴CF=BD=2BF,
∴CF=$\frac{2}{3}$BC=$\frac{2}{3}$AB=$\frac{2}{3}$×3=2.
点评 本题考查了全等三角形的判定和性质,等边三角形的性质,平行线的性质,解直角三角形,熟练掌握全等三角形的性质是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017届陕西省宝鸡市渭滨区九年级上学期期末考试数学试卷(解析版) 题型:单选题
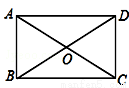
如图,矩形ABCD的对角线交于点O,若∠ACB=30°,AB=2,则OC的长为( )
A. 2 B. 3 C. 2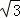 D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源:2017届云南省普洱市九年级学业水平测试模拟考试(一)数学试卷(解析版) 题型:判断题
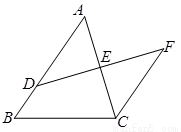
如图,D是△ABC的边AB上一点,E是AC的中点,过点C作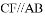 ,交DE的延长线于点F.求证:AD = CF.
,交DE的延长线于点F.求证:AD = CF.
查看答案和解析>>
科目:初中数学 来源:2017届山东省日照市莒县第三协作区九年级3月学业水平模拟考试数学试卷(解析版) 题型:解答题
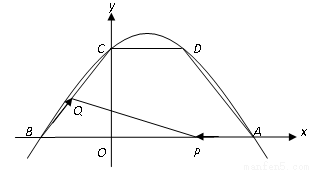
如图,抛物线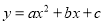 经过点A(5,0),B(-3,0),C(0,4).
经过点A(5,0),B(-3,0),C(0,4).
(1)求这条抛物线的函数关系式;
(2)过C作CD∥x轴交抛物线于D, 连续BC、AD,两个动点P、Q分别从A、B两点同时出发,都以每秒1个单位长度的速度运动.其中,点P沿着线段AB向B点运动,点Q沿着折线B→C→D的路线向D点运动.设这两个动点运动的时间为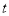 (秒)(0<
(秒)(0<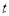 <7),△PQB的面积记为S.
<7),△PQB的面积记为S.
①求S与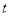 的函数关系式;
的函数关系式;
②当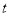 为何值时,S有最大值,最大值是多少?
为何值时,S有最大值,最大值是多少?
③是否存在这样的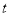 值,使得△PQB是直角三角形?若存在,请直接写出
值,使得△PQB是直角三角形?若存在,请直接写出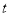 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2017届山东省日照市莒县第三协作区九年级3月学业水平模拟考试数学试卷(解析版) 题型:填空题
从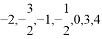 这七个数中,随机取出一个数,记为
这七个数中,随机取出一个数,记为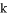 ,那么
,那么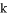 使关于
使关于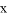 的函数
的函数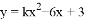 与
与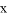 轴有交点,且使关于
轴有交点,且使关于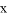 的不等式组
的不等式组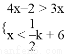 有且只有3个整数解的概率为___________ .
有且只有3个整数解的概率为___________ .
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
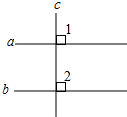 如图,已知a∥b,如果c⊥a,判断c与b的位置关系,并说明理由.
如图,已知a∥b,如果c⊥a,判断c与b的位置关系,并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com