
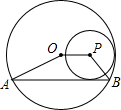
 如图,⊙P内切于⊙O,⊙O的弦AB与⊙P相切,且AB∥OP,若⊙O的半径为3,⊙P的半径为1,则四边形ABPO的面积为2$+2\sqrt{2}$.
如图,⊙P内切于⊙O,⊙O的弦AB与⊙P相切,且AB∥OP,若⊙O的半径为3,⊙P的半径为1,则四边形ABPO的面积为2$+2\sqrt{2}$. 分析 根据题意可知四边ABPO是梯形,可以得到OP、AB以及点P到AB的距离,从而可以求出四边形ABPO的面积.
解答 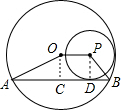 解:作OC⊥AB于点C,作PD⊥AB于点D,则点D为弦AB与⊙P的切点,如右图所示,
解:作OC⊥AB于点C,作PD⊥AB于点D,则点D为弦AB与⊙P的切点,如右图所示,
∵,⊙P内切于⊙O,⊙O的弦AB与⊙P相切,且AB∥OP,若⊙O的半径为3,⊙P的半径为1,
∴OP=3-1=2,PD=OC=1,四边形ABPO是梯形,
∵OC⊥AB,
∴AC=BC,AC=$\sqrt{O{A}^{2}-O{C}^{2}}=\sqrt{{3}^{2}-{1}^{2}}=2\sqrt{2}$,
∴AB=4$\sqrt{2}$,
∴四边形ABPO的面积是:(2+$4\sqrt{2}$)×1÷2=$2+2\sqrt{2}$,
故答案为:$2+2\sqrt{2}$.
点评 本题考查切线的性质、梯形的面积,解题的关键是明确题意,找出所求问题需要的条件,知道梯形的面积公式.


科目:初中数学 来源:2016-2017学年江苏省扬州市七年级下学期第一次月考数学试卷(解析版) 题型:填空题
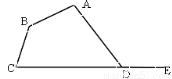
如图所示,在四边形ABCD中,∠A=80°,∠C=75°,∠ADE为四边形ABCD的一个外角,且∠ADE=125°,则∠B=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
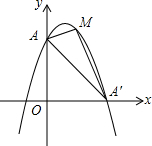 已知,抛物线y=-x2+2x+3与y轴交于A点与x轴正半轴交于A′,点M为第一象限内抛物线上的一动点,问:点M在何处时,△AMA′的面积最大,最大面积为多少.
已知,抛物线y=-x2+2x+3与y轴交于A点与x轴正半轴交于A′,点M为第一象限内抛物线上的一动点,问:点M在何处时,△AMA′的面积最大,最大面积为多少.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>0,bc>0 | B. | a<0,bc<0 | C. | a<0,bc>0 | D. | a>0,bc<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
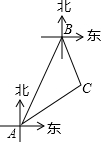 如图,点A、B是两个相距4000米的海岸观察点,点B位于点A的北偏东30°方向上,某日两观察点同时收到海面上的船C发出的信号,此时测得船C位于点A的北偏东60°方向上,位于点B的南偏东15°方向上,求此时船C到海岸AB的距离.(参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果精确到0.1米)
如图,点A、B是两个相距4000米的海岸观察点,点B位于点A的北偏东30°方向上,某日两观察点同时收到海面上的船C发出的信号,此时测得船C位于点A的北偏东60°方向上,位于点B的南偏东15°方向上,求此时船C到海岸AB的距离.(参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果精确到0.1米)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com