
����Ŀ���������x��һԪ���η���ax2+bx+c��0��2��ʵ������������һ��ʵ��������һ��ʵ������3������Ƹ÷���Ϊ��������������
��1������x2��4x+3��0�� �������̣�����x2��2x��3��0�� �������̣�������������������������
��2����֤�������㣨m��n���ڷ���������y![]() ��ʱ������x��һԪ���η���mx2+4x+n��0���������̣�
��ʱ������x��һԪ���η���mx2+4x+n��0���������̣�
��3��������ax2+bx+c��0���������̣�������P��3��2����Q��6��2�����ڶ��κ���y��ax2+bx+c�ϣ���ax2+bx+c��0����������
���𰸡���1���ǣ����ǣ���2������������3��x1��![]() , x2=
, x2=![]()
��������
��1���ֱ�ⷽ��x2-4x+3=0��x2-2x-3=0��������ǵĸ��������������������Ķ��壬�ж������Dz����������̣�
��2���ɵ㣨m��n���ڷ���������y=![]() ��ͼ���ϣ��õ�mn=3���ⷽ��mx2+4x+n=0���x1��x2��ֵ���ж��Dz����������̣�
��ͼ���ϣ��õ�mn=3���ⷽ��mx2+4x+n=0���x1��x2��ֵ���ж��Dz����������̣�
��3���ɷ���ax2+bx+c=0���������̣��õ�x1=3x2������������ͬ������P��3��2����Q��6��2������������y=ax2+bx+c�ϣ����������ߵĶԳ���õ�x1+x2��9���Ӷ�������̵���������
�⣺��1���ⷽ��x2-4x+3=0���ã�x1=3��x2=1��
��x1=3x2��
���x2-4x+3=0���������̣�
�ⷽ��x2-2x-3=0���ã�x1=3��x2=-1��
��x1=-3x2��
���x2-2x-3=0�����������̣�
�ʴ�Ϊ���ǣ����ǣ�
��2���ߵ㣨m,n���ڷ���������![]() �ϣ�����
�ϣ�����![]()
�������ʽ�ⷽ�̵ã�![]()
x1����![]() ��x2����
��x2����![]() ��
��
��x1��3x2��
���㣨m��n���ڷ���������y��![]() ��ʱ��һԪ���η���mx2+4x+n��0���������̣�
��ʱ��һԪ���η���mx2+4x+n��0���������̣�
��3���߷���ax2+bx+c��0���������̣�����x1��3x2��
��P��3��2����Q��6��2����������y��ax2+bx+c�ϣ�
�������ߵĶԳ���![]() ��
��
��x1+x2��9����3x2+x2��9����x2=![]() ����x1��3x2��
����x1��3x2��![]() ��
��
���Է���ax2+bx+c��0��������Ϊ��x1��![]() , x2=
, x2=![]()


 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ2������ABCD�У���A=60�㣬M��AD�ߵ��е㣬N��AB���ϵ�һ���㣬����AMN��MN����ֱ�߷��۵õ���A��MN������A��C����A��C���ȵ���Сֵ��( )
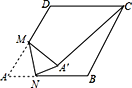
A. ![]() B.
B. ![]() -1C.
-1C. ![]() -1D.
-1D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB��90�㣬��A��60�㣬AC��2��D��AB����һ�����㣨�����A��B�غϣ���E��BC����һ�㣬�ҡ�CDE��30�㣮��AD��x��BE��y��������ͼ���У��ܱ�ʾy��x�ĺ�����ϵ��ͼ������ǣ�������
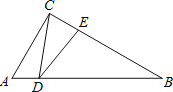
A.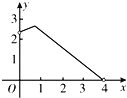 B.
B.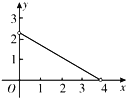 C.
C.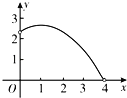 D.
D.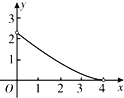
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �Ǩ�O��ֱ������
�Ǩ�O��ֱ������![]() �ڨ�O�ϣ�����C��������AB���ӳ��߽��ڵ�P������AC������O��OD��AC����O�ڵ�D������CD.����A=30����PC=6,��CD�ij�Ϊ
�ڨ�O�ϣ�����C��������AB���ӳ��߽��ڵ�P������AC������O��OD��AC����O�ڵ�D������CD.����A=30����PC=6,��CD�ij�Ϊ ![]() ����
����![]()

A. ![]() B.
B. ![]() C. 3D.
C. 3D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУΪ���꼶��ѧ������ѡ�ֹ����������ֽ�Ʒ������С�ʼDZ�ÿ��5Ԫ����ʼDZ�ÿ��7Ԫ���ֱ�ÿ֧10Ԫ������Ĵ�ʼDZ��������Ǹֱ�������2����������346Ԫ����ʹ����Ľ�Ʒ������࣬�������ֽ�Ʒ�У���ʼDZ������������____��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�E��AD���ϵ��е㣬����BE�����ӳ�BE��CD���ӳ����ڵ�F��
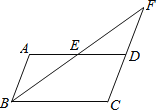
��1��֤����FD=AB����2����ƽ���ı���ABCD�����Ϊ8ʱ�����FED�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A�������ǣ�1��3��������A��ԭ��O˳ʱ����ת90���õ���A�������A������������ ��
A. ����3��1�� B. ��3����1�� C. ����1��3�� D. ��1����3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
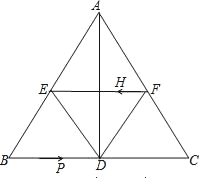
����Ŀ����ͼ������ABC�У�AB=AC��AD��BC�ڵ�D��BC=10cm��AD=8cm��E��F��ֱ�ΪAB��AC���е㣮
��1����֤���ı���AEDF�����Σ�
��2��������AEDF�������
��3����H��F����������߶�FE����ÿ��2cm���ٶ���E���˶�����P��B����������߶�BC����ÿ��3cm���ٶ���C���˶����ʵ�tΪ��ֵʱ���ı���BPHE��ƽ���ı��Σ���tȡ��ֵʱ���ı���PCFH��ƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У��Խ���AC��BD�ཻ�ڵ�O����E��BC���е㣬AE��BD�ڵ�F��BH��AE�ڵ�G������OG�������н����Т�OF��OH������AOF�ס�BGF����tan��GOH��2����FG+CH��![]() GO����ȷ�ĸ����ǣ�������
GO����ȷ�ĸ����ǣ�������
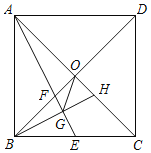
A. 1B. 2C. 3D. 4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com