练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，是☉O的直径，点在☉O上，过点C的切线与AB的延长线交于点P，连接AC，过点O作OD⊥AC交☉O于点D，连接CD.若∠A=30°，PC=6,则CD的长为 　　

    A. B. C. 3D.

    【答案】D

    【解析】

    连接OC，在Rt△POC中，根据∠P=30°，PC=6，求出OC，进而得出△DCO是等边三角形后解答即可．

    解：连接OC，

    ∵OA=OC，∠A=30°，
    ∴∠OCA=∠A=30°，
    ∴∠COB=∠A+∠ACO=60°，
    ∵PC是⊙O切线，
    ∴∠PCO=90°，∠P=30°，
    ∵PC=6，
    ∴OC=PCtan30°=2，
    ∵OD⊥AC，
    ∴∠AOD=60°，
    ∵∠COB=60°，
    ∴∠DOC=60°，
    ∵OD=OC，
    ∴△DOC是等边三角形，
    ∴CD=OC=2，
    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，一次函数y=kx+b的图象与反比例函数y=（x＞0）的图象交于A（2，﹣1）、B（，n）两点．直线y=2与y轴交于点C．

    1）求一次函数与反比例函数的解析式；

    2）求△ABC的面积；

    3）直接写出不等式kx+b＞在如图所示范围内的解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD，点O是边BC的中点，连接DO并延长，交AB的延长线于点E，连接BD、EC．

    （1）求证：四边形BECD是平行四边形；

    （2）若∠BOD＝100°，则当∠A＝　 　时，四边形BECD是矩形．

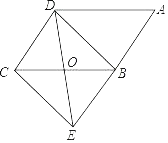
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O是△ABC的外接圆，AB是直径，过点O作OD⊥CB，垂足为点D，延长DO交⊙O于点E，过点E作PE⊥AB，垂足为点P，作射线DP交CA的延长线于F点，连接EF，

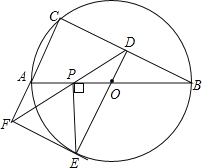
    （1）求证：OD＝OP；（2）求证：FE是⊙O的切线．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在⊙O中，AB是直径，AD是弦，∠ADE = 60°，∠C = 30°．

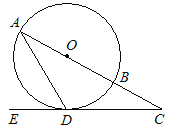
    ⑴判断直线CD是否是⊙O的切线，并说明理由；

    ⑵若CD = ，求BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，为矩形边上一点，连接，将沿翻折得到，过点作FG⊥BC于点G，若AB=4，FG=1，则AE的长度为____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果关于x的一元二次方程ax2+bx+c＝0有2个实数根，且其中一个实数根是另一个实数根的3倍，则称该方程为“立根方程”．

    （1）方程x2﹣4x+3＝0　 立根方程，方程x2﹣2x﹣3＝0　 立根方程；（请填“是”或“不是”）

    （2）请证明：当点（m，n）在反比例函数y上时，关于x的一元二次方程mx2+4x+n＝0是立根方程；

    （3）若方程ax2+bx+c＝0是立根方程，且两点P（3，2）、Q（6，2）均在二次函数y＝ax2+bx+c上，求方程ax2+bx+c＝0的两个根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】校园空地上有一面墙，长度为20m，用长为32m的篱笆和这面墙围成一个矩形花圃，如图所示．

    （1）能围成面积是126m2的矩形花圃吗？若能，请举例说明；若不能，请说明理由．

    （2）若篱笆再增加4m，围成的矩形花圃面积能达到170m2吗？请说明理由．

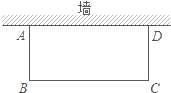
    查看答案和解析>>

    科目：初中数学 来源： 题型：

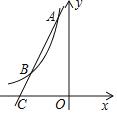
    【题目】已知反比例函数与一次函数y＝kx+b（k≠0）交于点A（﹣1，6）、B（n，2）．

    （1）求反比例函数与一次函数的表达式；

    （2）若点A关于y轴的对称点为A′，连接AA′，BA′，求△AA′B的面积．

    查看答案和解析>>

    同步练习册答案