
【题目】已知:如图①,直线MN⊥直线PQ,垂足为O,点A在射线OP上,点B在射线OQ上(A、B不与O点重合),点C在射线ON上且OC=2,过点C作直线![]() ∥PQ,点D在点C的左边且CD=3.
∥PQ,点D在点C的左边且CD=3.
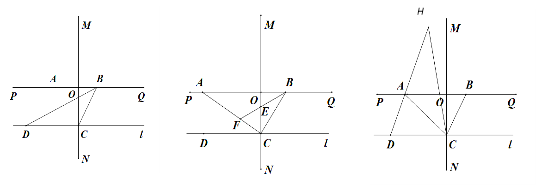
(1) 直接写出△BCD的面积.
(2) 如图②,若AC⊥BC,作∠CBA的平分线交OC于E,交AC于F,则∠CEF与∠CFE有何数量关系?请说明理由.
(3) 如图③,若∠ADC=∠DAC,点B在射线OQ上运动,∠ACB的平分线交DA的延长线于点H,在点B运动过程中![]() 的值是否变化?若不变,直接写出其值;若变化,直接写出变化范围.
的值是否变化?若不变,直接写出其值;若变化,直接写出变化范围.
【答案】(1)、3;(2)、∠CEF=∠CFE;(3)、![]()
【解析】
试题分析:(1)、根据三角形的面积计算公式求出三角形的面积;(2)、根据垂直得出∠BCO=∠BAC,根据角平分线得出∠ABF=∠CBF,则∠ABF+∠BAC=∠CBF+∠BCO,根据△ABF和△BCE的内角和定理得出∠AFB=∠CEB,从而得出答案;(3)、根据题意求出![]() 的大小.
的大小.
试题解析:(1)、S△BCD=3
(2)、∠CEF=∠CFE
理由:∵AC⊥BC,MN⊥AB ∴∠BAC+∠ABC=90°,∠BCO+∠ABC=90°, ∴∠BCO+∠ABC=∠BAC+∠ABC,
∴∠BCO =∠BAC, ∵BF平分∠CBA ∴∠ABF=∠CBF ∴∠ABF+∠BAC =∠CBF+∠BCO
在△ABF与△BCE中 ∠ABF+∠BAC +∠AFB =∠CBF+∠BCA+∠CEB=1800
∴∠AFB=∠CEB ∴∠CEF=∠CFE
(3)、![]() =
=![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知:线段AB=20cm.
(1)如图1,点P沿线段AB自A点向B点以2厘米/秒运动,点P出发2秒后,点Q沿线段BA自B点向A点以3厘米/秒运动,问再经过几秒后P、Q相距5cm?
(2)如图2:AO=4cm,PO=2cm,∠POB=60°,点P绕着点O以60度/秒的速度逆时针旋转一周停止,同时点Q沿直线BA自B点向A点运动,假若点P、Q两点能相遇,求点Q运动的速度.
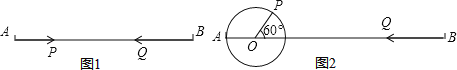
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.
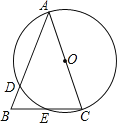
(1)求证:BE=CE;
(2)若BD=2,BE=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)已知:如图,AD⊥BC于D,EG⊥BC与G,∠E=∠3,试问:AD是∠BAC的平分线吗?若是,请说明理由.(在横线上填写正确的依据或证明步骤)
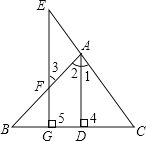
解答:是,理由如下:
∵AD⊥BC,EG⊥BC(已知)
∴∠4=∠5=90°(垂直的定义)
∴AD∥EG
∴∠1=∠E
∠2=∠3
∵∠E=∠3(已知)
∴∠ =∠ ;
∴AD是∠BAC的平分线(角平分线的定义).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角△ABC中,∠ACB=90°,O是AB边上的中点,点D、E分别在AC、BC边上,且∠DOE=90°,DE交OC于P,下列结论:
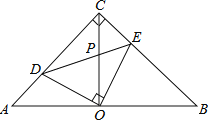
①图中的全等三角形共有3对;
②AD=CE;
③∠CDO=∠BEO;
④OC=DC+CE;
⑤△ABC的面积是四边形DOEC面积的2倍.
正确的是 .(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在扇形OAB中,半径OA=4,∠AOB=120°,点C在![]() 上,OD⊥AC于点D,OE⊥BC于点E,当点C从点A运动到点B时,线段DE长度的变化情况是( )
上,OD⊥AC于点D,OE⊥BC于点E,当点C从点A运动到点B时,线段DE长度的变化情况是( )
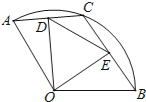
A.先变小,后变大
B.先变大,后变小
C.DE与OD的长度保持相等
D.固定不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形ABCD的顶点O在坐标原点,点B的坐标为(1,4),点A在第二象限,反比例函数y=![]() 的图象经过点A,则k的值是( )
的图象经过点A,则k的值是( )
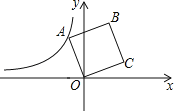
A.﹣2 B.﹣4 C.﹣![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com