
【题目】如图,在平面直角坐标系中,正方形ABCD的顶点O在坐标原点,点B的坐标为(1,4),点A在第二象限,反比例函数y=![]() 的图象经过点A,则k的值是( )
的图象经过点A,则k的值是( )
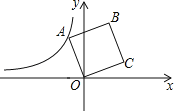
A.﹣2 B.﹣4 C.﹣![]() D.
D.![]()
【答案】C
【解析】
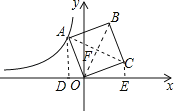
试题分析:作AD⊥x轴于D,CE⊥x轴于E,先通过证得△AOD≌△OCE得出AD=OE,OD=CE,设A(x,![]() ),则C(
),则C(![]() ,﹣x),根据正方形的性质求得对角线解得F的坐标,根据直线OB的解析式设出直线AC的解析式为:y=﹣
,﹣x),根据正方形的性质求得对角线解得F的坐标,根据直线OB的解析式设出直线AC的解析式为:y=﹣![]() x+b,代入交点坐标求得解析式,然后把A,C的坐标代入即可求得k的值.
x+b,代入交点坐标求得解析式,然后把A,C的坐标代入即可求得k的值.
解:作AD⊥x轴于D,CE⊥x轴于E,
∵∠AOC=90°,
∴∠AOD+∠COE=90°,
∵∠AOD+∠OAD=90°,
∴∠OAD=∠COE,
在△AOD和△OCE中,
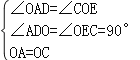 ,
,
∴△AOD≌△OCE(AAS),
∴AD=OE,OD=CE,
设A(x,![]() ),则C(
),则C(![]() ,﹣x),
,﹣x),
∵点B的坐标为(1,4),
∴OB=![]() =
=![]() ,
,
直线OB为:y=4x,
∵AC和OB互相垂直平分,
∴它们的交点F的坐标为(![]() ,2),
,2),
设直线AC的解析式为:y=﹣![]() x+b,
x+b,
代入(![]() ,2)得,2=﹣
,2)得,2=﹣![]() ×
×![]() +b,解得b=
+b,解得b=![]() ,
,
直线AC的解析式为:y=﹣![]() x+
x+![]() ,
,
把A(x,![]() ),C(
),C(![]() ,﹣x)代入得
,﹣x)代入得
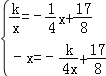 ,解得k=﹣
,解得k=﹣![]() .
.
故选C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:如图①,直线MN⊥直线PQ,垂足为O,点A在射线OP上,点B在射线OQ上(A、B不与O点重合),点C在射线ON上且OC=2,过点C作直线![]() ∥PQ,点D在点C的左边且CD=3.
∥PQ,点D在点C的左边且CD=3.
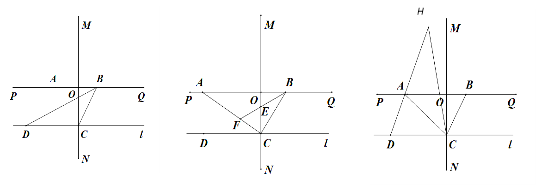
(1) 直接写出△BCD的面积.
(2) 如图②,若AC⊥BC,作∠CBA的平分线交OC于E,交AC于F,则∠CEF与∠CFE有何数量关系?请说明理由.
(3) 如图③,若∠ADC=∠DAC,点B在射线OQ上运动,∠ACB的平分线交DA的延长线于点H,在点B运动过程中![]() 的值是否变化?若不变,直接写出其值;若变化,直接写出变化范围.
的值是否变化?若不变,直接写出其值;若变化,直接写出变化范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和B港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB为直角,∠AOC为锐角,且OM平分∠BOC,ON平分∠AOC.
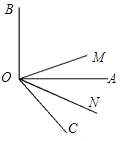
(1)如果∠AOC=50°,求∠MON的度数.
(2)如果∠AOC为任意一个锐角,你能求出∠MON的度数吗?若能,请求出来,若不能,说明为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图有A、B、C、D、E五个居民点,每天产生的垃圾量(单位:吨),交通状况和每相邻两个居民点的距离如图所示,现要建一座垃圾中转站(只能建在A、B、C、D、E的其中一处),这五个居民点的垃圾都运到此中转站,那么中转站建在何处,才能使总的运输量最小?(圆圈内的数字为垃圾量,线段上的字母表示距离,b<a<c).中转站应建在 处.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com