
分析 (1)(2)观察已知的等式,发现:等式的左边是连续自然数的立方和,等式的右边是连续自然数的和的平方;由此得出答案即可;
(3)根据(1)中发现的结论,即可求得结论.
解答 解:(1)$\frac{1}{4}$n2(n+1)2;
(2)13+23+33+…+1003=$\frac{1}{4}$×1002×1012=25502500;
(3)①原式=13+23+33+…+993+1003-(13+23+33+43+…203)=$\frac{1}{4}$×1002×1012-$\frac{1}{4}$×202×212=25458400;
②原式=23×(13+23+33++…503=8×$\frac{1}{4}$×502×512=13005000.
点评 此题考查数字的变化规律,找出数字的变化规律,利用规律解决问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
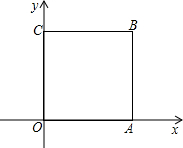 如图所示,正方形OABC的顶点为O(0,0),A(1,0),B(1,1),C(0,1).
如图所示,正方形OABC的顶点为O(0,0),A(1,0),B(1,1),C(0,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
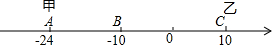 已知数轴上有A、B、C三点,分别代表-24,-10,10,两只电子蚂蚁甲、乙分别从A、C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.
已知数轴上有A、B、C三点,分别代表-24,-10,10,两只电子蚂蚁甲、乙分别从A、C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com