
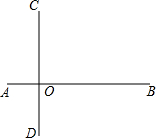 如图,已知AB⊥CD于点D,点E为平面内一点,且∠BOE=60°.
如图,已知AB⊥CD于点D,点E为平面内一点,且∠BOE=60°.分析 (1)首先根据题意画出图形,由AB⊥CD,可知然后∠COB=90°,图1中有∠EOC=∠COB+∠BOE;图2中有∠EOC=∠COB-∠BOE;
(2)如图3,因为OF平分∠COE,∠COF=75°,从而可知∠FOB=15°,因为OG平分∠BOE,可求得∠BOG=30°,可求得∠FOG=45°;如图4;∠COE=30°,根据角平分线的定义可知∠COF=15°,∠BOG=30°,从而可知∠FOG=45°;
(3如图3,由角平分线的性质可知:∠COF=45$°+\frac{1}{2}α$,从而可求得∠FOB=45°-$\frac{1}{2}α$,由角平分线的定义可知∠BOG=$\frac{1}{2}$∠BOE=$\frac{1}{2}α$,∠FOG=45°;如图4;∠COE=90°-∠EOB=90°-α,由角平分线的定义可知∠COF=45$°-\frac{1}{2}α$,∠BOG=$\frac{1}{2}α$,∠FOG=45°.
解答 解:(1)如图1、2所示: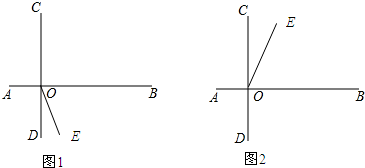
∵AB⊥CD,
∴∠COB=90°.
如图1,∠EOC=∠COB+∠BOE=90°+60°=150°,
如图2,∠EOC=∠COB-∠BOE=90°-60°=30°.
(2)如图3、4所示;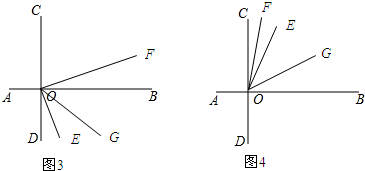
如图3,∵OF平分∠COE,
∴∠COF=$\frac{1}{2}∠COE$=75°.
∴∠FOB=90°-75°=15°.
∵OG平分∠BOE,
∴∠BOG=$\frac{1}{2}∠BOE$=30°,
∴∠FOG=15°+30°=45°.
如图4;∠COE=90°-∠EOB=90°-60°=30°,
∵OF平分∠COE,
∴∠COF=$\frac{1}{2}∠COE$=15°.
∵OG平分∠BOE,
∴∠BOG=$\frac{1}{2}∠BOE$=30°,
∴∠FOG=15°+30°=45°.
(3)如(2)中图3、4所示:
如图3所示:
∵OF平分∠COE,
∴∠COF=$\frac{1}{2}∠COE$=$\frac{1}{2}(90°+α)$=45$°+\frac{1}{2}α$.
∴∠FOB=90°-$\frac{1}{2}∠COE$=90°-45°-$\frac{1}{2}α$=45°-$\frac{1}{2}α$.
∵OG平分∠BOE,
∴∠BOG=$\frac{1}{2}$∠BOE=$\frac{1}{2}α$,
∴∠FOG=45°-$\frac{1}{2}α$+$\frac{1}{2}α$=45°
如图4;∠COE=90°-∠EOB=90°-α,
∵OF平分∠COE,
∴∠COF=$\frac{1}{2}∠COE$=$\frac{1}{2}$(90°-α)=45$°-\frac{1}{2}α$.
∵OG平分∠BOE,
∴∠BOG=$\frac{1}{2}α$,
∴∠FOG=45$°-\frac{1}{2}α$+$\frac{1}{2}α$=45°.
综上所述,∠FOG=45°,对于α<90°恒成立.
点评 本题主要考查的是角平分线的定义和垂直的定义,掌握角平分线的定义是解题的关键.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:选择题
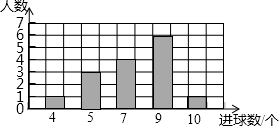 某篮球兴趣小组有15名同学,在一次投篮比赛中,他们的成绩如右面的条形图所示.这15名同学进球数的众数和中位数分别是( )
某篮球兴趣小组有15名同学,在一次投篮比赛中,他们的成绩如右面的条形图所示.这15名同学进球数的众数和中位数分别是( )| A. | 10,7 | B. | 7,7 | C. | 9,9 | D. | 9,7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com