
【题目】由点P(14,1),A(a,0),B(0,a)确定的△PAB的面积为18.
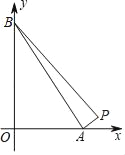
(1)如图,若0<a<14,求a的值.
(2)如果a>14,请画图并求a的值.
【答案】(1)a1=3,a2=12;(2)a=![]() .
.
【解析】
(1)当0<a<14时,作PD⊥x轴于点D,由P(14,1),A(a,0),B(0,a)就可以表示出△ABP的面积,建立关于a的方程求出其解即可;
(2)当a>14时,作PD⊥x轴于点D,由P(14,1),A(a,0),B(0,a)就可以表示出△ABP的面积,建立关于a的方程求出其解即可.
(1)当0<a<14时,
如图,作PD⊥x轴于点D,
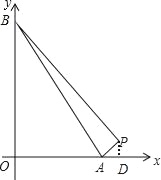
∵P(14,1),A(a,0),B(0,a),
∴PD=1,OD=14,OA=a,OB=a,
∴S△PAB=S梯形OBPD﹣S△OAB﹣S△ADP=![]() ×14(a+1)﹣
×14(a+1)﹣![]() a2﹣
a2﹣![]() ×1×(14﹣a)=18,
×1×(14﹣a)=18,
解得:a1=3,a2=12;
(2)当a>14时,如图,
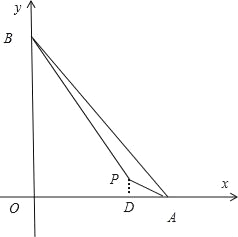
作PD⊥x轴于点D,
∵P(14,1),A(a,0),B(0,a),
∴PD=1,OD=14,OA=a,OB=a,
∴S△PAB=S△OAB﹣S梯形OBPD﹣S△ADP=![]() a2﹣
a2﹣![]() ×14(a+1)﹣
×14(a+1)﹣![]() ×1×(a﹣14)=18,
×1×(a﹣14)=18,
解得:a1=![]() ,a2=
,a2=![]() (不合题意,舍去);
(不合题意,舍去);
∴a=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
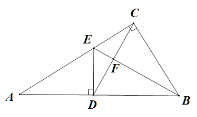
【题目】如图,在Rt△ABC中,∠ACB=![]() ,D是AB边上的一点,过D作DE⊥AB交AC于点E,BC=BD,连结CD交BE于点F.
,D是AB边上的一点,过D作DE⊥AB交AC于点E,BC=BD,连结CD交BE于点F.
(1)求证:CE=DE;
(2)若点D为AB的中点,求∠AED的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,D是BC的中点. 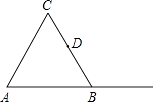
(1)作图: ①过B作AC的平行线BH;
②过D作BH的垂线,分别交AC,BH,AB的延长线于E,F,G.
(2)在图中找出一对全等的三角形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列方程:
(1)![]() =3.
=3.
(2)(y+2)2=(3y﹣1)2.
(3)(x﹣2)(x+5)=8.
(4)(2x+1)2=﹣6x﹣3.
(5)2x2﹣3x﹣2=0.
(6)4x2﹣12x﹣1=0(配方法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△CED均为等边三角形,且B,C,D三点共线.线段BE,AD相交于点O,AF⊥BE于点F.若OF=1,则AF的长为( )
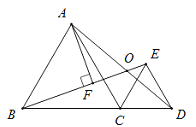
A. 1 B. ![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,D是BC的中点. 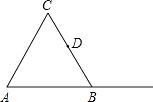
(1)作图: ①过B作AC的平行线BH;
②过D作BH的垂线,分别交AC,BH,AB的延长线于E,F,G.
(2)在图中找出一对全等的三角形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
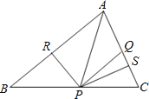
【题目】如图,在△ABC中,点P是BC上一点,PR⊥AB,PS⊥AC,垂足分别为点R、S,PR=PS,点Q是AC上一点,且AQ=PQ,
(1)求证:QP∥AR;
(2)AR、AS相等吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品经销店欲购进A、B两种纪念品,用320元购进的A种纪念品与用400元购进的B种纪念品的数量相同,每件B种纪念品的进价比A种纪念品的进价贵10元.
(1)求A、B两种纪念品每件的进价分别为多少?
(2)若该商店A种纪念品每件售价45元,B种纪念品每件售价60元,这两种纪念品共购进200件,这两种纪念品全部售出后总获利不低于1600元,求A种纪念品最多购进多少件.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com