
【题目】(1)已知∠AOB=25°42′,则∠AOB的余角为 ,∠AOB的补角为 ;
(2)已知∠AOB=α,∠BOC=β,OM平分∠AOB,ON平分∠BOC,用含α,β的代数式表示∠MON的大小;
(3)如图,若线段OA与OB分别为同一钟表上某一时刻的时针与分针,且∠AOB=25°,则经过多少时间后,△AOB的面积第一次达到最大值.

【答案】(1)64°18′,154°18′;(2)∠MON=![]() ;(3)
;(3)![]() 分
分
【解析】
(1)依据余角和补角的定义即可求出∠AOB的余角和补角;
(2)依据角平分线的定义表示出∠AOM=∠BOM=![]() ∠AOB=
∠AOB=![]() α,∠CON=∠BON=
α,∠CON=∠BON=![]() ∠COB=
∠COB=![]() β,最后再依据∠MON与这些角的关系求解即可;(3)当OA⊥OB时面积最大,此时∠AOB=90°,根据角的和差关系可得求出三角形OBC面积第一次达到最大的时间.
β,最后再依据∠MON与这些角的关系求解即可;(3)当OA⊥OB时面积最大,此时∠AOB=90°,根据角的和差关系可得求出三角形OBC面积第一次达到最大的时间.
解:(1)∵∠AOB=25°42',
∴∠AOB的余角=90°﹣25°42'=64°18′,
∠AOB的补角=180°﹣25°42'=154°18′;
故答案为:64°18′,154°18′;
(2)
①如图1:
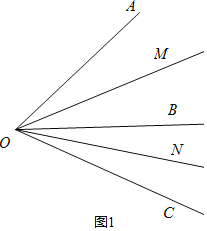
∵∠AOB=α,∠BOC=β
∴∠AOC=∠AOB+∠BOC=90°+30°=120°
∵OM平分∠AOB,ON平分∠BOC,
∴∠AOM=∠BOM=![]() ∠AOB=
∠AOB=![]() α,∠CON=∠BON=
α,∠CON=∠BON=![]() ∠COB=
∠COB=![]() β,
β,
∴∠MON=∠BOM+∠CON=![]() ;
;
②如图2,

∠MON=∠BOM﹣∠BON=![]() ;
;
③如图3,

∠MON=∠BON﹣∠BOM=![]() .
.
∴∠MON为![]() 或
或![]() 或
或![]() .
.
(3)当OA⊥OB时,△AOB的面积第一次达到最大值,此时∠AOB=90°,
设经过x分钟后,△AOB的面积第一次达到最大值,
根据题意得:6x+25﹣![]() ×30=90,
×30=90,
解得x=![]() .
.


科目:初中数学 来源: 题型:
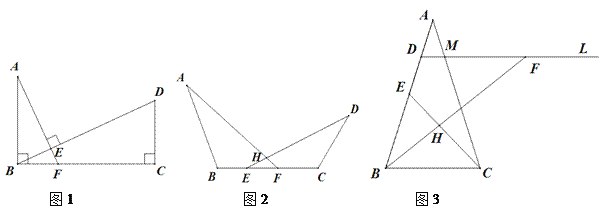
【题目】(1)【特殊发现】如图1,AB⊥BC于B,CD⊥BC于C,连接BD,过A作AF⊥BD,交BD于E,交BC于F,若BF=1,BC=3,则AB·CD= ;
(2)【类比探究】如图2,在线段BC上存在点E,F,连接AF,DE交于点H,若∠ABC=∠AHD=∠ECD,求证:AB·CD=BF·CE;
(3)【解决问题】如图3,在等腰△ABC中,AB=AC=4,E为AB中点,D为AE中点,过点D作直线DM∥BC,在直线DM上取一点F,连接BF交CE于点H,使∠FHC=∠ABC,问:DF·BC是否为定值?若是,请求出,若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
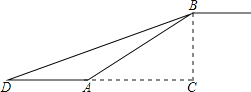
【题目】如图,在合肥地铁3号线某站通道的建设中,建设工人将坡长为20米![]() 米
米![]() 、坡角为
、坡角为![]() 的斜坡通道改造成坡角为
的斜坡通道改造成坡角为![]() 的斜坡通道,使斜坡的起点从点A处向左平移至点D处,求改造后的斜坡通道BD的长
的斜坡通道,使斜坡的起点从点A处向左平移至点D处,求改造后的斜坡通道BD的长![]() 结果精确到
结果精确到![]() 米
米![]() 参考数据:
参考数据: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点A、B,与双曲线
轴分别交于点A、B,与双曲线![]() (
(![]() <0)分别交于点C、D,且C点的坐标为(
<0)分别交于点C、D,且C点的坐标为(![]() ,2).
,2).
⑴分别求出直线AB及双曲线的解析式;
⑵求出点D的坐标;
⑶利用图象直接写出:当x在什么范围内取值时, ![]() >
>![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】滴滴快车是一种便捷的出行工具,其计价规则如图:

(注:滴滴快车车费由里程费、时长费、远途费三部分构成,其中里程费按行车的具体时段标准和实际里程计算:时长费按具体时段标准和行车的实际时间计算,远途费的收取方式:行车里程10公里以内(含10公里)不收远途费,超过10公里的,超出部分每公里收0.3元)
(1)小红早上7:00从家出发乘坐滴滴快车到学校,行驶里程2公里,用时8分钟,需付车费 元,傍晚17:00放学乘坐滴滴快车到妈妈单位,行驶里程5公里,用时20分钟,需付车费 元;
(2)某人06:10出发,乘坐滴滴快车到某地,行驶里程20公里,用时40分钟,需付车费多少元?
(3)某人普通时段乘坐演滴快车到某地,用时30分钟,共花车费39.8元,求他行驶的里程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中, ![]() 的直角边AC在x轴上,
的直角边AC在x轴上, ![]() ,反比例函数
,反比例函数![]() 的图象经过BC边的中点
的图象经过BC边的中点![]() .
.
![]() 求这个反比例函数的表达式;
求这个反比例函数的表达式;
![]() 若
若![]() 与
与![]() 成中心对称,且
成中心对称,且![]() 的边FG在y轴的正半轴上,点E在这个函数的图象上.
的边FG在y轴的正半轴上,点E在这个函数的图象上.
![]() 求OF的长;
求OF的长;
![]() 连接
连接![]() ,证明四边形ABEF是正方形.
,证明四边形ABEF是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上面一层有一个圆圈,
以下各层均比上一层多一个圆圈,一共堆了n 层.将图1倒置后与原图1拼成图2的形状,这样我们可以
算出图1中所有圆圈的个数为1+2+3+…+n=![]() .
.
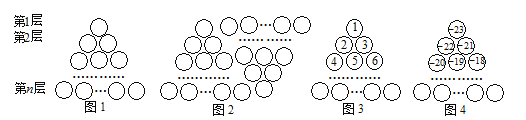
如果图中的圆圈共有13层,请解决下列问题:
(1)我们自上往下,在每个圆圈中按图3的方式填上一串连续的正整数1,2,3,4,……,则最底层最左
边这个圆圈中的数是 ;
(2)我们自上往下,在每个圆圈中按图4的方式填上一串连续的整数-23,-22,-21,-20,……,求
最底层最右边圆圈内的数是_______;
(3)求图4中所有圆圈中各数的绝对值之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)和正比例函数y=![]() x的图象如图所示,则方程ax2+(b﹣
x的图象如图所示,则方程ax2+(b﹣![]() )x+c=0(a≠0)的两根之和( )
)x+c=0(a≠0)的两根之和( )

A. 大于0 B. 等于0 C. 小于0 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象交
的图象交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() .
.

(1)求二次函数的解析式和直线![]() 的解析式;
的解析式;
(2)点![]() 是直线
是直线![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的垂线,交抛物线于点
轴的垂线,交抛物线于点![]() ,当点
,当点![]() 在第一象限时,求线段
在第一象限时,求线段![]() 长度的最大值;
长度的最大值;
(3)在抛物线上是否存在异于![]() 的点
的点![]() ,使
,使![]() 中
中![]() 边上的高为
边上的高为![]() ,若存在求出点
,若存在求出点![]() 的坐标;若不存在请说明理由.
的坐标;若不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com