
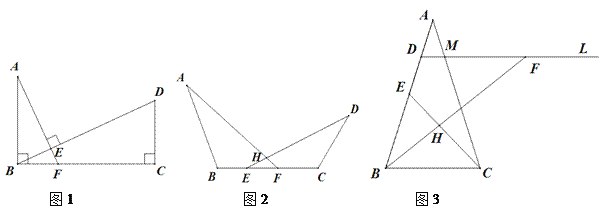
【题目】(1)【特殊发现】如图1,AB⊥BC于B,CD⊥BC于C,连接BD,过A作AF⊥BD,交BD于E,交BC于F,若BF=1,BC=3,则AB·CD= ;
(2)【类比探究】如图2,在线段BC上存在点E,F,连接AF,DE交于点H,若∠ABC=∠AHD=∠ECD,求证:AB·CD=BF·CE;
(3)【解决问题】如图3,在等腰△ABC中,AB=AC=4,E为AB中点,D为AE中点,过点D作直线DM∥BC,在直线DM上取一点F,连接BF交CE于点H,使∠FHC=∠ABC,问:DF·BC是否为定值?若是,请求出,若不是,请说明理由.
【答案】(1)3;(2)详见解析;(3)是,DF·BC=12,理由详见解析.
【解析】试题分析:(1)先由余角的性质得到∠A=∠CBD,从而△ABF∽△BCD,再根据相似三角形的性质列比例式求解;(2)由∠ABC=∠AHD=∠ECD,得到∠AFB=∠EDC,从而△ABF∽△ECD,
再根据相似三角形的性质列比例式求解;(3)法一,在DA的延长线上取一点N,使∠DNF=∠ABC,然后由△FDN∽△ABC和△NFB∽△BEC,得到![]() 和
和![]() ,然后整理即可得到结论;法二,取BC的中点K,连接EK,由E为AB中点,然后由△FDB∽△EKC,得到
,然后整理即可得到结论;法二,取BC的中点K,连接EK,由E为AB中点,然后由△FDB∽△EKC,得到![]() ,然后结合法一整理即可得到结论;法三,延长FD,CE交于点G,由法一得:∠ADM=∠AMD,∠ABF=∠ECB,然后由△GMC∽△BDF和△GED∽△CEB,得到
,然后结合法一整理即可得到结论;法三,延长FD,CE交于点G,由法一得:∠ADM=∠AMD,∠ABF=∠ECB,然后由△GMC∽△BDF和△GED∽△CEB,得到![]() 和
和![]() ,然后整理即可得到结论;
,然后整理即可得到结论;
解: (1) ∵AB⊥BC,AF⊥BD,
∴∠A+∠AFB=90°, ∠CBD+∠AFB=90°,
∴∠A=∠CBD,
又∵∠ABF=∠C,
∴△ABF∽△BCD,
![]() ,
,
∴ AB·CD=BC·BF=3.
(2)容易由∠ABC=∠AHD=∠ECD,得到∠AFB=∠EDC,
从而△ABF∽△ECD,
那么AB·CD=BF·CE;
(3)法一:(模型法)解:是,DF·BC=12,
理由如下:
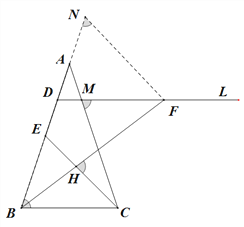
如图,在DA的延长线上取一点N,使∠DNF=∠ABC,
由AB=AC,DM∥BC,可得:∠ADM=∠AMD=∠ABC=∠ACB∠FMC=∠DNF,
∴△FDN∽△ABC,且DF=NF,∴![]() 即NF·BC=ND·AB,
即NF·BC=ND·AB,
又由∠ABC=∠FHC,得∠ABF+∠FBC=∠FBC+∠ECB,
∴∠ABF=∠ECB,∴△NFB∽△BEC,
∴![]() 即NF·BC=NB·BE,
即NF·BC=NB·BE,
∴NB·BE=ND·AB,依题意得:AD=DE=1,BE=2,
∴NB·2=ND·4,∴NB=2ND,∴ND=BD=3,
∴NB=6,∴NF·BC=6×2=12即DF·BC=12。
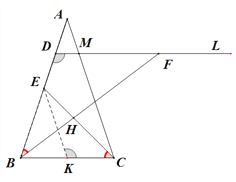
法二:(平行法)取BC的中点K,连接EK,由E为AB中点,
∴EK![]()
![]() AC,得∠ADM=∠ABC=∠EKB,
AC,得∠ADM=∠ABC=∠EKB,
∴∠BDF=∠EKC,再由法一可知:∠DBF=∠ECB,
∴△FDB∽△EKC,∴![]() ,即DF·CK=EK·DB,
,即DF·CK=EK·DB,
由法一得:DB=3,EK=BE=2,CK=![]() BC,
BC,
∴DF·![]() BC=2×3,∴DF·BC=12。
BC=2×3,∴DF·BC=12。
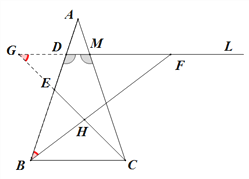
法三:延长FD,CE交于点G,由法一得:∠ADM=∠AMD,∠ABF=∠ECB,
∴∠BDM=∠CMD,又∵DF∥BC,∴∠G=∠ECB,∴∠G=∠ABF,
∴△GMC∽△BDF,∴![]() ,∴DF·GM=MC·DB=3×3=9,
,∴DF·GM=MC·DB=3×3=9,
又∵GD∥BC,DE=1,BE=2,
∴△GED∽△CEB,∴![]() ,
,
同理![]() ,∴GM=GD+DM=
,∴GM=GD+DM=![]() BC+
BC+![]() BC=
BC=![]() BC,
BC,
∴DF·![]() BC=9,∴DF·BC=12。
BC=9,∴DF·BC=12。


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案科目:初中数学 来源: 题型:
【题目】请从以下两个小题中任选一题作答,若多选,则按第一题计分.
(A)儿童节期间,文具商店搞促销活动,同时购买一个书包和一个文具盒可以打8折优惠,能比标价省13.2元,已知书包标价比文具盒标价的3倍少6元.那么设一个文具盒标价为x元,依据题意列方程得________.
(B)用科学记算器计算: ![]() ________(计算结果保留两位小数).
________(计算结果保留两位小数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,AM是△ACD的外角∠DAF的平分线.

(1)求证:AM是⊙O的切线;
(2)若∠D = 60°,AD = 2,射线CO与AM交于N点,请写出求ON长的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
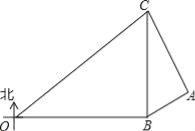
【题目】在某次海上军事学习期间,我军为确保△OBC海域内的安全,特派遣三艘军舰分别在O、B、C处监控△OBC海域,在雷达显示图上,军舰B在军舰O的正东方向80海里处,军舰C在军舰B的正北方向60海里处,三艘军舰上装载有相同的探测雷达,雷达的有效探测范围是半径为r的圆形区域.(只考虑在海平面上的探测)
(1)若三艘军舰要对△OBC海域进行无盲点监控,则雷达的有效探测半径r至少为多少海里?
(2)现有一艘敌舰A从东部接近△OBC海域,在某一时刻军舰B测得A位于北偏东60°方向上,同时军舰C测得A位于南偏东30°方向上,求此时敌舰A离△OBC海域的最短距离为多少海里?
(3)若敌舰A沿最短距离的路线以20![]() 海里/小时的速度靠近△OBC海域,我军军舰B沿北偏东15°的方向行进拦截,问B军舰速度至少为多少才能在此方向上拦截到敌舰A?
海里/小时的速度靠近△OBC海域,我军军舰B沿北偏东15°的方向行进拦截,问B军舰速度至少为多少才能在此方向上拦截到敌舰A?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当k值相同时,我们把正比例函数![]() 与反比例函数
与反比例函数![]() 叫做“关联函数”.
叫做“关联函数”.
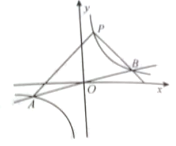
(1)如图,若k>0,这两个函数图象的交点分别为A,B,求点A,B的坐标(用k表示);
(2)若k=1,点P是函数![]() 在第一象限内的图象上的一个动点(点P不与B重合),设点P的坐标为(
在第一象限内的图象上的一个动点(点P不与B重合),设点P的坐标为(![]() ),其中m>0且m≠2.作直线PA,PB分别与x轴交于点C,D,则△PCD是等腰三角形,请说明理由;
),其中m>0且m≠2.作直线PA,PB分别与x轴交于点C,D,则△PCD是等腰三角形,请说明理由;
(3)在(2)的基础上,是否存在点P使△PCD为直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备用9万元购进50台电视机,为了节省费用,学校打算以出厂价从厂家直接采购,已知厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元.
(1)若学校同时购进其中两种不同型号电视机共50台,用去9万元,请研究一下学校的采购方案;
(2)若学校去商场购买,在出厂价相同的情况下,商场销售一台甲种电视机获利150元,销售一台乙种电视机获利200元,销售一台丙种电视机获利250元,在(1)的条件下,学校选择哪种方案省下的钱最多?
(3)若学校准备用9万元同时购进三种不同的电视机50台,请你设计进货方案(直接写出方案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社会团体准备购进甲、乙两种防护服捐给一线抗疫人员,经了解,购进5件甲种防护服和4件乙种防护服需要2万元,购进10件甲种防护服和3件乙种防护服需要3万元.
(1)甲种防护服和乙种防护服每件各多少元?
(2)实际购买时,发现厂家有两种优惠方案,方案一:购买甲种防护服超过20件时,超过的部分按原价的8折付款,乙种防护服没有优惠;方案二:两种防护服都按原价的9折付款,该社会团体决定购买![]()
![]() 件甲种防护服和30件乙种防护服.
件甲种防护服和30件乙种防护服.
①求两种方案的费用![]() 与件数
与件数![]() 的函数解析式;
的函数解析式;
②请你帮该社会团体决定选择哪种方案更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在AC上,点F、G分别在AC、BC的延长线上,CE平分∠ACB交BD于点O,且∠EOD+∠OBF=180°,∠F=∠G.则图中与∠ECB相等的角有( )
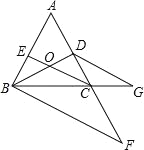
A. 6个 B. 5个 C. 4个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知∠AOB=25°42′,则∠AOB的余角为 ,∠AOB的补角为 ;
(2)已知∠AOB=α,∠BOC=β,OM平分∠AOB,ON平分∠BOC,用含α,β的代数式表示∠MON的大小;
(3)如图,若线段OA与OB分别为同一钟表上某一时刻的时针与分针,且∠AOB=25°,则经过多少时间后,△AOB的面积第一次达到最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com