
【题目】学校准备用9万元购进50台电视机,为了节省费用,学校打算以出厂价从厂家直接采购,已知厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元.
(1)若学校同时购进其中两种不同型号电视机共50台,用去9万元,请研究一下学校的采购方案;
(2)若学校去商场购买,在出厂价相同的情况下,商场销售一台甲种电视机获利150元,销售一台乙种电视机获利200元,销售一台丙种电视机获利250元,在(1)的条件下,学校选择哪种方案省下的钱最多?
(3)若学校准备用9万元同时购进三种不同的电视机50台,请你设计进货方案(直接写出方案)
【答案】(1)学校的采购方案是购买甲种型号的电视机25台和乙种型号的电视机25台或购买甲种型号的电视机35台和丙种型号的电视机15台;
(2)学校选择购买甲种型号的电视机25台和乙种型号的电视机25台这种方案更省钱;
(3)有四种购买方案,方案一:购买甲种型号的电视机27台,购买乙种型号的电视剧20台,购买丙种型号的电视机3台;方案二:购买甲种型号的电视机29台,购买乙种型号的电视剧15台,购买丙种型号的电视机6台;购买甲种型号的电视机31台,购买乙种型号的电视剧10台,购买丙种型号的电视机9台;方案四:购买甲种型号的电视机33台,购买乙种型号的电视剧5台,购买丙种型号的电视机12台.
【解析】
(1)根据题意可以利用分类讨论的数学思想列出各种情况,写出各种情况相应的方程,从而可以解答本题;
(2)根据(1)中的结果可以计算出商场的获利,然后比较大小即可解答本题;
(3)根据题意可以列出相应的三元一次方程组,注意x、y、z都是正整数,从而可以解答本题.
解:(1)设学校购买甲种型号的电视机x台,购买乙种型号的电视剧y台,购买丙种型号的电视机z台,
若学校购买甲种型号的电视机和乙种型号的电视机,
![]() ,得
,得![]() ,
,
若学校购买甲种型号的电视机和丙种型号的电视机,
![]() ,得
,得![]() ,
,
若学校购买乙种型号的电视机和丙种型号的电视机,
![]() ,得
,得![]() (舍去),
(舍去),
答:学校的采购方案是购买甲种型号的电视机25台和乙种型号的电视机25台或购买甲种型号的电视机35台和丙种型号的电视机15台;
(2)当购买甲种型号的电视机25台和乙种型号的电视机25台时,
商场获利为:150×25+200×25=8750(元),
当购买甲种型号的电视机35台和丙种型号的电视机15台时,
商场获利为:150×35+250×15=9000(元),
∵8750<9000,
∴学校选择购买甲种型号的电视机25台和乙种型号的电视机25台这种方案更省钱,
答:学校选择购买甲种型号的电视机25台和乙种型号的电视机25台这种方案更省钱;
(3)设学校购买甲种型号的电视机x台,购买乙种型号的电视剧y台,购买丙种型号的电视机z台,
![]() ,
,
解得,![]() 或
或![]() 或
或![]() 或
或![]() ,
,
答:有四种购买方案,
方案一:购买甲种型号的电视机27台,购买乙种型号的电视剧20台,购买丙种型号的电视机3台,
方案二:购买甲种型号的电视机29台,购买乙种型号的电视剧15台,购买丙种型号的电视机6台,
方案三:购买甲种型号的电视机31台,购买乙种型号的电视剧10台,购买丙种型号的电视机9台,
方案四:购买甲种型号的电视机33台,购买乙种型号的电视剧5台,购买丙种型号的电视机12台.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】如图,已知A(0,a),B(0,b),C(m,b)且(a-4)2+|b+3|=0,S△ABC=14。

(1)求C点的坐标
(2)作DE⊥DC交y轴于E点,EF为∠AED的平分线,且∠DFE=90o。求证:FD平分∠ADO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD的周长为24,∠ABC=60°,以AB为腰在菱形外作底角为45°的等腰△ABE,连结AC,CE,则△ACE的面积为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
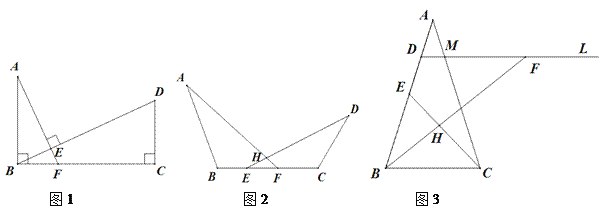
【题目】(1)【特殊发现】如图1,AB⊥BC于B,CD⊥BC于C,连接BD,过A作AF⊥BD,交BD于E,交BC于F,若BF=1,BC=3,则AB·CD= ;
(2)【类比探究】如图2,在线段BC上存在点E,F,连接AF,DE交于点H,若∠ABC=∠AHD=∠ECD,求证:AB·CD=BF·CE;
(3)【解决问题】如图3,在等腰△ABC中,AB=AC=4,E为AB中点,D为AE中点,过点D作直线DM∥BC,在直线DM上取一点F,连接BF交CE于点H,使∠FHC=∠ABC,问:DF·BC是否为定值?若是,请求出,若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 的正方形方格中,每个小正方形的边长都为1,顶点都在网格线交点处的三角形,
的正方形方格中,每个小正方形的边长都为1,顶点都在网格线交点处的三角形, ![]() 是一个格点三角形.
是一个格点三角形.
![]() 在图
在图![]() 中,请判断
中,请判断![]() 与
与![]() 是否相似,并说明理由;
是否相似,并说明理由;
![]() 在图
在图![]() 中,以O为位似中心,再画一个格点三角形,使它与
中,以O为位似中心,再画一个格点三角形,使它与![]() 的位似比为2:1
的位似比为2:1
![]() 在图
在图![]() 中,请画出所有满足条件的格点三角形,它与
中,请画出所有满足条件的格点三角形,它与![]() 相似,且有一条公共边和一个公共角.
相似,且有一条公共边和一个公共角.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果两个一次函数![]() 和
和![]() 满足
满足![]() ,那么称这两个一次函数为“平行一次函数”.
,那么称这两个一次函数为“平行一次函数”.
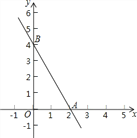
如图,已知函数![]() 的图象与x轴、y轴分别交于A、B两点,一次函数
的图象与x轴、y轴分别交于A、B两点,一次函数![]() 与
与![]() 是“平行一次函数”
是“平行一次函数”
![]() 若函数
若函数![]() 的图象过点
的图象过点![]() ,求b的值;
,求b的值;
![]() 若函数
若函数![]() 的图象与两坐标轴围成的三角形和
的图象与两坐标轴围成的三角形和![]() 构成位似图形,位似中心为原点,位似比为1:2,求函数
构成位似图形,位似中心为原点,位似比为1:2,求函数![]() 的表达式.
的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2-4ax+b交x轴正半轴于A、B两点,交y轴正半轴于C,且OB=OC=3.
(1) 求抛物线的解析式;
(2) 如图1,D为抛物线的顶点,P为对称轴左侧抛物线上一点,连接OP交直线BC于G,连GD.是否存在点P,使![]() ?若存在,求点P的坐标;若不存在,请说明理由;
?若存在,求点P的坐标;若不存在,请说明理由;
(3) 如图2,将抛物线向上平移m个单位,交BC于点M、N.若∠MON=45°,求m的值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中, ![]() 的直角边AC在x轴上,
的直角边AC在x轴上, ![]() ,反比例函数
,反比例函数![]() 的图象经过BC边的中点
的图象经过BC边的中点![]() .
.
![]() 求这个反比例函数的表达式;
求这个反比例函数的表达式;
![]() 若
若![]() 与
与![]() 成中心对称,且
成中心对称,且![]() 的边FG在y轴的正半轴上,点E在这个函数的图象上.
的边FG在y轴的正半轴上,点E在这个函数的图象上.
![]() 求OF的长;
求OF的长;
![]() 连接
连接![]() ,证明四边形ABEF是正方形.
,证明四边形ABEF是正方形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com