
【题目】如图,抛物线y=ax2-4ax+b交x轴正半轴于A、B两点,交y轴正半轴于C,且OB=OC=3.
(1) 求抛物线的解析式;
(2) 如图1,D为抛物线的顶点,P为对称轴左侧抛物线上一点,连接OP交直线BC于G,连GD.是否存在点P,使![]() ?若存在,求点P的坐标;若不存在,请说明理由;
?若存在,求点P的坐标;若不存在,请说明理由;
(3) 如图2,将抛物线向上平移m个单位,交BC于点M、N.若∠MON=45°,求m的值.


【答案】(1)y=x2-4x+3 ;(2) P(![]() );(3)
);(3) ![]()
【解析】分析:(1)把![]() ,
,![]() ,代入
,代入![]() ,解方程组即可.
,解方程组即可.
(2)如图1中,连接OD、BD,对称轴交x轴于K,将![]() 绕点O逆时针旋转90°得到△OCG,则点G在线段BC上,只要证明
绕点O逆时针旋转90°得到△OCG,则点G在线段BC上,只要证明![]() 是等腰直角三角形,即可得到直线GO与抛物线的交点即为所求的点P.利用方程组即可解决问题. (3)如图2中,将
是等腰直角三角形,即可得到直线GO与抛物线的交点即为所求的点P.利用方程组即可解决问题. (3)如图2中,将![]() 绕点O顺时针旋转
绕点O顺时针旋转![]() 得到
得到![]() ,首先证明
,首先证明![]() ,设
,设![]() ,
,![]() ,则
,则![]() ,
,
设平移后的抛物线的解析式为![]() ,由
,由![]() 消去y得到
消去y得到![]() ,由
,由 ,推出
,推出![]() ,
,![]() ,M、N关于直线
,M、N关于直线![]() 对称,所以
对称,所以![]() ,设
,设![]() ,则
,则![]() ,利用勾股定理求出a以及MN的长,再根据根与系数关系,列出方程即可解决问题.
,利用勾股定理求出a以及MN的长,再根据根与系数关系,列出方程即可解决问题.
本题解析:
(1)![]() ,
,![]() ,
,![]() ,代入
,代入![]() ,
,
得![]() ,解得
,解得![]() ,
,
∴抛物线的解析式为![]()
(2)如图1中,连接OD、BD,对称轴交x轴于K.
由题意![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
将![]() 绕点O逆时针旋转90°得到
绕点O逆时针旋转90°得到![]() ,则点G在线段BC上,
,则点G在线段BC上,![]() ,
,![]() ,
,![]() ,
,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,
∴直线GO与抛物线的交点即为所求的点P.
设直线OD的解析式为![]() ,把D点坐标代入得到,/span>
,把D点坐标代入得到,/span>![]() ,
,![]() ,
,
∴直线OD的解析式为![]() ,
,![]() ,
,
∴直线OG的解析式为![]() ,
,
由![]() 解得
解得![]() 或
或 ,
,![]() 点P在对称轴左侧,
点P在对称轴左侧,![]() 点P坐标为
点P坐标为![]()
(3)如图2中,将![]() 绕点O顺时针旋转90°得到
绕点O顺时针旋转90°得到![]()

![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,
设平移后的抛物线的解析式为![]() ,
,
由 消去y得到
消去y得到![]() ,
,
![]() ,
,![]() ,
,
∴M、N关于直线![]() 对称,
对称,![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,
,![]() (负根已经舍弃),
(负根已经舍弃),![]() ,
,![]() ,
,![]()


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】
(1)在数轴上表示下列各数:0,–2.5,![]() ,–2,+5,
,–2,+5,![]() .
.
![]()
(2)将上列各数用“<”连接起来:___________ _____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备用9万元购进50台电视机,为了节省费用,学校打算以出厂价从厂家直接采购,已知厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元.
(1)若学校同时购进其中两种不同型号电视机共50台,用去9万元,请研究一下学校的采购方案;
(2)若学校去商场购买,在出厂价相同的情况下,商场销售一台甲种电视机获利150元,销售一台乙种电视机获利200元,销售一台丙种电视机获利250元,在(1)的条件下,学校选择哪种方案省下的钱最多?
(3)若学校准备用9万元同时购进三种不同的电视机50台,请你设计进货方案(直接写出方案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的集合里.
﹣|﹣![]() |,0,
|,0,![]() ,﹣(﹣3.14),2006,﹣(+5),+1.88,
,﹣(﹣3.14),2006,﹣(+5),+1.88,
(1)正数集合:{ …};
(2)负数集合:{ …};
(3)整数集合:{ …};
(4)分数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在AC上,点F、G分别在AC、BC的延长线上,CE平分∠ACB交BD于点O,且∠EOD+∠OBF=180°,∠F=∠G.则图中与∠ECB相等的角有( )
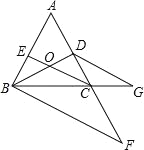
A. 6个 B. 5个 C. 4个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某民营企业准备用14000元从外地购进A、B两种商品共600件,其中A种商品的成本价为20元,B种商品的成本价为30元.
(1)该民营企业从外地购得A、B两种商品各多少件?
(2)该民营企业计划租用甲、乙两种货车共6辆,一次性将A、B两种商品运往某城市,已知每辆甲种货车最多可装A种商品110件和B种商品20件;每辆乙种货车最多可装A种商品30件和B种商品90件,问安排甲、乙两种货车有几种方案?请你设计出具体的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)先化简,再求值:当(x﹣2)2+|y+1|=0时,求代数式4(![]() x2﹣3xy﹣y2)﹣3(x2﹣7xy﹣2y2)的值;
x2﹣3xy﹣y2)﹣3(x2﹣7xy﹣2y2)的值;
(2)关于x的代数式(x2+2x)﹣[kx2﹣(3x2﹣2x+1)]的值与x无关,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题:
(1) (﹣8) +3=__ (2) ﹣3﹣6= __ (3) ﹣3×2= __ (4) ﹣9÷(﹣3) =__
(5) 0×(﹣2019) =__ (6) ![]() (7) (2)2×32= (8) (2)3÷(﹣1)5 =
(7) (2)2×32= (8) (2)3÷(﹣1)5 =
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com