
【题目】如图,已知A(0,a),B(0,b),C(m,b)且(a-4)2+|b+3|=0,S△ABC=14。

(1)求C点的坐标
(2)作DE⊥DC交y轴于E点,EF为∠AED的平分线,且∠DFE=90o。求证:FD平分∠ADO.
【答案】(1)(4,-3);(2)见解析;
【解析】
(1)根据平方根的性质和绝对值的非负性,求出a,b的值,再根据三角形面积公式即可解答.
(2)根据角平分线的性质,三角形的内角和定理,分别求出∠OEG=∠FDG和∠ADF=∠AEF即可求证.
(1)∵(a-4)2+|b+3|=0,
∴a=4,b=-3.
又∵S△ABC =14,
∴![]() × AB×BO=14,
× AB×BO=14,
∵AB=7
∴BC=4,C点的坐标为(4,-3);
(2)设OD与EF相交于点G,

∵∠F=90°,∠EOG=90°,
∴∠EGO=∠FGD,
∴∠OEG=∠FDG①,
∵∠ADE=90°,
∴∠ADF+∠FDE=90°,在△EFD中,∠FDE+∠FED=90°,
∴∠ADF=∠FED,
又∵EF平分∠AED,
∴∠AEF=∠FED,∴∠ADF=∠AEF②,
由①②得∠FDG=∠ADF,
∴FD平分∠ADO.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣3)﹣(﹣2)+(﹣4);
(2)﹣10+14+16﹣8;
(3)(-4)×(-5)-90÷(-15);
(4)﹣23÷![]() ×(﹣
×(﹣![]() )2;
)2;
(5)(![]() +
+![]() ﹣
﹣![]() )×(﹣36);
)×(﹣36);
(6)﹣14﹣![]() ×[2﹣(﹣3)2]
×[2﹣(﹣3)2]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解:
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.
中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以为顶点作一个70°角,角的两边分别交AB,AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
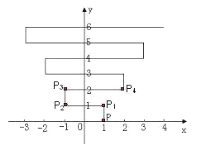
【题目】如下图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位…,依此规律跳动下去,点P第2019次跳动至点P2019的坐标是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请从以下两个小题中任选一题作答,若多选,则按第一题计分.
(A)儿童节期间,文具商店搞促销活动,同时购买一个书包和一个文具盒可以打8折优惠,能比标价省13.2元,已知书包标价比文具盒标价的3倍少6元.那么设一个文具盒标价为x元,依据题意列方程得________.
(B)用科学记算器计算: ![]() ________(计算结果保留两位小数).
________(计算结果保留两位小数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】身高1.65米的兵兵在建筑物前放风筝,风筝不小心挂在了树上.在如图所示的平面图形中,矩形CDEF代表建筑物,兵兵位于建筑物前点B处,风筝挂在建筑物上方的树枝点G处(点G在FE的延长线上).经测量,兵兵与建筑物的距离BC=5米,建筑物底部宽FC=7米,风筝所在点G与建筑物顶点D及风筝线在手中的点A在同一条直线上,点A距地面的高度AB=1.4米,风筝线与水平线夹角为37°.
(1)求风筝距地面的高度GF;
(2)在建筑物后面有长5米的梯子MN,梯脚M在距墙3米处固定摆放,通过计算说明:若兵兵充分利用梯子和一根米长的竹竿能否触到挂在树上的风筝?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
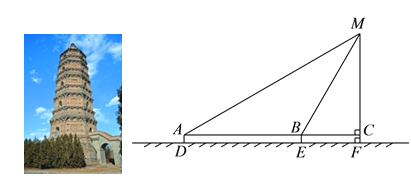
【题目】某校九年级数学兴趣小组的同学进行社会实践活动时,想利用所学的解直角三角形的知识测量某塔的高度,他们先在点![]() 用高
用高![]() 米的测角仪
米的测角仪![]() 测得塔顶
测得塔顶![]() 的仰角为
的仰角为![]() ,然后沿
,然后沿![]() 方向前行
方向前行![]() m到达点
m到达点![]() 处,在
处,在![]() 处测得塔顶
处测得塔顶![]() 的仰角为
的仰角为![]() .请根据他们的测量数据求此塔
.请根据他们的测量数据求此塔![]() 的高.(结果精确到
的高.(结果精确到![]() m,参考数据:
m,参考数据: ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
(1)在数轴上表示下列各数:0,–2.5,![]() ,–2,+5,
,–2,+5,![]() .
.
![]()
(2)将上列各数用“<”连接起来:___________ _____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备用9万元购进50台电视机,为了节省费用,学校打算以出厂价从厂家直接采购,已知厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元.
(1)若学校同时购进其中两种不同型号电视机共50台,用去9万元,请研究一下学校的采购方案;
(2)若学校去商场购买,在出厂价相同的情况下,商场销售一台甲种电视机获利150元,销售一台乙种电视机获利200元,销售一台丙种电视机获利250元,在(1)的条件下,学校选择哪种方案省下的钱最多?
(3)若学校准备用9万元同时购进三种不同的电视机50台,请你设计进货方案(直接写出方案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com