
【题目】某社会团体准备购进甲、乙两种防护服捐给一线抗疫人员,经了解,购进5件甲种防护服和4件乙种防护服需要2万元,购进10件甲种防护服和3件乙种防护服需要3万元.
(1)甲种防护服和乙种防护服每件各多少元?
(2)实际购买时,发现厂家有两种优惠方案,方案一:购买甲种防护服超过20件时,超过的部分按原价的8折付款,乙种防护服没有优惠;方案二:两种防护服都按原价的9折付款,该社会团体决定购买![]()
![]() 件甲种防护服和30件乙种防护服.
件甲种防护服和30件乙种防护服.
①求两种方案的费用![]() 与件数
与件数![]() 的函数解析式;
的函数解析式;
②请你帮该社会团体决定选择哪种方案更合算.
【答案】(1)甲种防护服每件2400元,乙种防护服每件2000元;(2)①![]()
![]() ,
,![]() ,②当购买甲种防护服65件时,两种方案一样;当购买甲种防护服的,件数超过20件而少于65件时,选择方案二更合算;当购买甲种防,护服的件数多于65件时,选择方案一更合算.
,②当购买甲种防护服65件时,两种方案一样;当购买甲种防护服的,件数超过20件而少于65件时,选择方案二更合算;当购买甲种防,护服的件数多于65件时,选择方案一更合算.
【解析】
(1)根据题意列二元一次方程组即可求解;
(2)①根据题意找出两种方案的函数关系式即可;②分三种情况进行比较即可.
解:(1)设甲种防护服每件![]() 元,乙种防护服每件
元,乙种防护服每件![]() 元,
元,
根据题意,得![]()
解得![]()
答:甲种防护服每件2400元,乙种防护服每件2000元.
(2)①方案一:
![]()
![]()
方案二:
![]()
②当![]() 时,
时,
即:![]()
解得:![]()
∴当![]() 时
时
即:![]() ,解得
,解得![]() ;
;
当![]() 时,
时,
即:![]() ,解得
,解得![]() .
.
∴当购买甲种防护服65件时,两种方案一样;当购买甲种防护服的件数超过20件而少于65件时,选择方案二更合算;当购买甲种防护服的件数多于65件时,选择方案一更合算.


科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,△ADC与△ABC关于直线AC对称,AE与CD垂直交BC的延长线于点E,∠EAF=45°,且AF与AB在AE的两侧,EF⊥AF.
(1)依题意补全图形.
(2)①在AE上找一点P,使点P到点B,点C的距离和最短;
②求证:点D到AF,EF的距离相等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,
(1)写出数轴上点B表示的数 ;
(2)|5﹣3|表示5与3之差的绝对值,实际上也可理解为5与3两数在数轴上所对的两点之间的距离.如|x﹣3|的几何意义是数轴上表示有理数x的点与表示有理数3的点之间的距离.试探索:
①:若|x﹣8|=2,则x= .
②:|x+12|+|x﹣8|的最小值为 .
(3)动点P从O点出发,以每秒5个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.求当t为多少秒时?A,P两点之间的距离为2;
(4)动点P,Q分别从O,B两点,同时出发,点P以每秒5个单位长度沿数轴向右匀速运动,Q点以P点速度的两倍,沿数轴向右匀速运动,设运动时间为t(t>0)秒.问当t为多少秒时?P,Q之间的距离为4.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
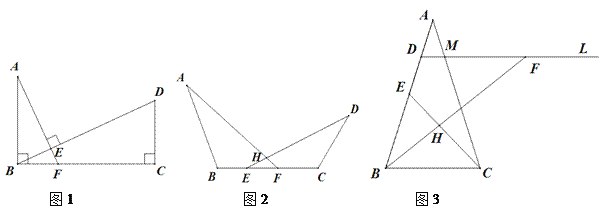
【题目】(1)【特殊发现】如图1,AB⊥BC于B,CD⊥BC于C,连接BD,过A作AF⊥BD,交BD于E,交BC于F,若BF=1,BC=3,则AB·CD= ;
(2)【类比探究】如图2,在线段BC上存在点E,F,连接AF,DE交于点H,若∠ABC=∠AHD=∠ECD,求证:AB·CD=BF·CE;
(3)【解决问题】如图3,在等腰△ABC中,AB=AC=4,E为AB中点,D为AE中点,过点D作直线DM∥BC,在直线DM上取一点F,连接BF交CE于点H,使∠FHC=∠ABC,问:DF·BC是否为定值?若是,请求出,若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣5,1),B(﹣2,2),C(﹣1,4),请按下列要求画图:
(1)将△ABC先向右平移4个单位长度、再向下平移1个单位长度,得到△A1B1C1,画出△A1B1C1;
(2)画出与△ABC关于原点O成中心对称的△A2B2C2,并直接写出点A2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果两个一次函数![]() 和
和![]() 满足
满足![]() ,那么称这两个一次函数为“平行一次函数”.
,那么称这两个一次函数为“平行一次函数”.
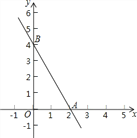
如图,已知函数![]() 的图象与x轴、y轴分别交于A、B两点,一次函数
的图象与x轴、y轴分别交于A、B两点,一次函数![]() 与
与![]() 是“平行一次函数”
是“平行一次函数”
![]() 若函数
若函数![]() 的图象过点
的图象过点![]() ,求b的值;
,求b的值;
![]() 若函数
若函数![]() 的图象与两坐标轴围成的三角形和
的图象与两坐标轴围成的三角形和![]() 构成位似图形,位似中心为原点,位似比为1:2,求函数
构成位似图形,位似中心为原点,位似比为1:2,求函数![]() 的表达式.
的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有理数a、b在数轴上的对应点如图所示.
(1)已知a=–2.3,b=0.4,计算|a+b|–|a|–|1–b|的值;
(2)已知有理数a、b,计算|a+b|–|a|–|1–b|的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
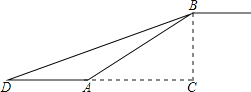
【题目】如图,在合肥地铁3号线某站通道的建设中,建设工人将坡长为20米![]() 米
米![]() 、坡角为
、坡角为![]() 的斜坡通道改造成坡角为
的斜坡通道改造成坡角为![]() 的斜坡通道,使斜坡的起点从点A处向左平移至点D处,求改造后的斜坡通道BD的长
的斜坡通道,使斜坡的起点从点A处向左平移至点D处,求改造后的斜坡通道BD的长![]() 结果精确到
结果精确到![]() 米
米![]() 参考数据:
参考数据: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
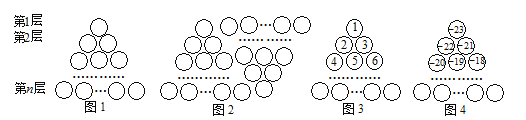
【题目】图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上面一层有一个圆圈,
以下各层均比上一层多一个圆圈,一共堆了n 层.将图1倒置后与原图1拼成图2的形状,这样我们可以
算出图1中所有圆圈的个数为1+2+3+…+n=![]() .
.
如果图中的圆圈共有13层,请解决下列问题:
(1)我们自上往下,在每个圆圈中按图3的方式填上一串连续的正整数1,2,3,4,……,则最底层最左
边这个圆圈中的数是 ;
(2)我们自上往下,在每个圆圈中按图4的方式填上一串连续的整数-23,-22,-21,-20,……,求
最底层最右边圆圈内的数是_______;
(3)求图4中所有圆圈中各数的绝对值之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com