练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣5，1），B（﹣2，2），C（﹣1，4），请按下列要求画图：

    （1）将△ABC先向右平移4个单位长度、再向下平移1个单位长度，得到△A1B1C1，画出△A1B1C1；

    （2）画出与△ABC关于原点O成中心对称的△A2B2C2，并直接写出点A2的坐标．

    【答案】（1）画图形如图所示见解析，（2）画图形如图所示见解析，点A2（5，-1）

    【解析】

    （1）将三个顶点分别向右平移4个单位长度、再向下平移1个单位长度，得到对应点，再顺次连接即可得；

    （2）将△ABC的三个顶点关于原点O成中心对称的对称点，再顺次连接可得．

    （1）画图形如图所示，

    （2）画图形如图所示，点A2（5，-1）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】我县盛产绿色蔬菜，生产销售一种绿色蔬菜，若在市场上直接销售，每吨利润为800元，经粗加工销售，每吨利润可达2000元，经精加工后销售，每吨利润涨至2500元．我县一家农工商公司采购这种蔬菜若干吨生产销售，若单独进行精加工，需要30天才能完成，若单独进行粗加工，需要20天才能完成．已知每天单独粗加工比单独精加工多生产10吨．

    （1）试问这家农工商公司采购这种蔬菜共多少吨？

    （2）由于两种加工方式不能同时进行受季节条件限制，公司必须在24天内将这批蔬菜全部销售或加工完毕，为此该公司研制了三种可行方案：

    方案一：将蔬菜全部进行粗加工；

    方案二：尽可能多的对蔬菜进行精加工，没有来得及进行加工的蔬菜，在市场上直接销售；

    方案三：将部分蔬菜进行精加工，其余蔬菜进行粗加工，并恰好24天完成，你认为选择哪种方案获利最多？请通过计算说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列图形中，既是轴对称图形又是中心对称图形的是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，为了测量某建筑物BC的高度，小明先在地面上用测角仪自A处测得建筑物顶部的仰角是30°，然后在水平地而上向建筑物前进了50m到达D处，此时遇到一斜坡，坡度i=1： ，沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°，（坡度i=1： 是指坡面的铅直高度FE与水平宽度DE的比）．请你计算出该建筑物BC的高度．（取 =1.732，结果精确到0.1m）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，CN是等边△的外角内部的一条射线，点A关于CN的对称点为D，连接AD，BD，CD，其中AD，BD分别交射线CN于点E，P．

    （1）依题意补全图形；

    （2）若，求的大小（用含的式子表示）；

    （3）用等式表示线段， 与之间的数量关系，并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】南博汽车城销售某种型号的汽车，每辆进货价为25万元，市场调研表明：当销售价为29万元时，平均每周能售出8辆，而当销售价每降低0.5万元时，平均每周能多售出4辆．如果设每辆汽车降价x万元，每辆汽车的销售利润为y万元．（销售利润=销售价﹣进货价）

    （1）求y与x的函数关系式；在保证商家不亏本的前提下，写出x的取值范围；
    （2）假设这种汽车平均每周的销售利润为z万元，试写出z与x之间的函数关系式；
    （3）当每辆汽车的定价为多少万元时，平均每周的销售利润最大，最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，比例规是一种画图工具，它由长度相等的两脚AC和BD交叉构成，利用它可以把线段按一定的比例伸长或缩短．如果把比例规的两脚合上，使螺丝钉固定在刻度3的地方（即同时使OA=3OC，OB=3OD），然后张开两脚，使A，B两个尖端分别在线段a的两个端点上，当CD=1.8cm时，则AB的长为（ ）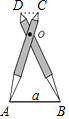
    A.7.2 cm
    B.5.4 cm
    C.3.6 cm
    D.0.6 cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】新农村社区改造中，有一部分楼盘要对外销售，某楼盘共23层，销售价格如下：第八层楼房售价为4000元/米2，从第八层起每上升一层，每平方米的售价提高50元；反之，楼层每下降一层，每平方米的售价降低30元，已知该楼盘每套楼房面积均为120米2．

    若购买者一次性付清所有房款，开发商有两种优惠方案：

    方案一：降价8%，另外每套楼房赠送a元装修基金；

    方案二：降价10%，没有其他赠送．

    （1）请写出售价y（元/米2）与楼层x（1≤x≤23，x取整数）之间的函数关系式；

    （2）老王要购买第十六层的一套楼房，若他一次性付清购房款，请帮他计算哪种优惠方案更加合算．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线1上有A，B两点，AB=12cm，点O是线段AB上的一点，OA=2OB．

    （1）OA=______cm，OB=______cm；

    （2）若点C是线段AB上一点（点C不与点AB重合），且满足AC=CO+CB，求CO的长；

    （3）若动点P，Q分别从A，B同时出发，向右运动，点P的速度为2cm/s，点Q的速度为1cm/s．设运动时间为t（s），当点P与点Q重合时，P，Q两点停止运动．求当t为何值时，2OP-OQ=4（cm）；

    查看答案和解析>>

    同步练习册答案