
【题目】如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E、F两点,连结DE,已知∠B=30°,⊙O的半径为6,弧DE的长度为2π.
(1)求证:DE∥BC;
(2)若AF=CE,求线段BC的长度.
【答案】
(1)
解:连接OD、OE,

设∠EOD=n°,
∵弧DE的长度为2π,
∴2π= ![]() ,
,
∴n=60°,
∴△EOD是等边三角形,
∴∠ODE=60°,
∵AB是⊙O的切线,
∴∠ODA=90°
∴∠EAD=30°,
∴∠B=∠EAD,
∴ED∥BC,
(2)
解:连接FD,

由(1)可知ED∥BC,
∴∠AED=∠C=90°,
∴由圆周角定理可知:FD是⊙O的直径,
∴∠AFD=30°,
∴cos∠AFD= ![]() ,DF=12
,DF=12
∴AF=8 ![]() ,
,
∵cos∠AFD= ![]() ,
,
∴EF=6 ![]() ,
,
∴CE=AF=8 ![]() ,
,
∴AE=CF=2 ![]() ,
,
∴AC=10 ![]() ,
,
∵tanB= ![]() ,
,
∴BC=30,
【解析】(1)连接OD、OE,根据弧DE的长度为2π,从而可求出∠EOD的度数,根据切线的性质即可求出∠EDA的度数,从可得出∠B=∠EAD;(2)连接FD,由圆周角定理可知FD是⊙O的直径,从而可知∠AFD=30°,从而可求出AF、AE的长度,再由tanB= ![]() 即可求出BC的长度.
即可求出BC的长度.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=45°,∠ACB=60°,AB=3 ![]() ,点D为BA延长线上的一点,且∠D=∠ACB,⊙O为△ACD的外接圆.
,点D为BA延长线上的一点,且∠D=∠ACB,⊙O为△ACD的外接圆. 
(1)求BC的长;
(2)求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,点A,B,C表示的数分别是-6,10,12.点A以每秒3个单位长度的速度向右运动,同时线段BC以每秒1个单位长度的速度也向右运动.
(1)运动前线段AB的长度为________;
(2)当运动时间为多长时,点A和线段BC的中点重合?
(3)试探究是否存在运动到某一时刻,线段AB=![]() AC?若存在,求出所有符合条件的点A表示的数;若不存在,请说明理由.
AC?若存在,求出所有符合条件的点A表示的数;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从仓库O出发在东西街道上运送水果,规定向东为正方向,一次到达的5个销售地点依次分别为A,B,C,D,E,最后回到仓库O,货车行驶的记录(单位:千米)如下:+1,+3,﹣6,﹣1,﹣2,+5.请问:
(1)请以仓库O为原点,向东为正方向,选择适当的单位长度,画出数轴,并标出A,B,C,D,E的位置;
(2)试求出该货车共行驶了多少千米?
(3)如果货车运送的水果以100千克为标准重量,超过的千克数记为正数,不足的千克数记为负数,则运往A,B,C,D,E五个地点的水果重量可记为:
+50,﹣15,+25,﹣10,﹣15,则该货车运送的水果总重量是多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,则∠A、∠C、∠E、∠F满足的数量关系是( )

A. ∠A=∠C+∠E+∠F B. ∠A+∠E﹣∠C﹣∠F=180°
C. ∠A﹣∠E+∠C+∠F=90° D. ∠A+∠E+∠C+∠F=360°
查看答案和解析>>
科目:初中数学 来源: 题型:
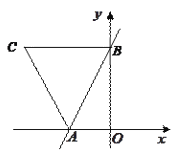
【题目】如图,已知一次函数![]() 的图像与x轴、
的图像与x轴、![]() 轴分别交于点A、B,且BC∥AO,梯形AOBC的面积为10.
轴分别交于点A、B,且BC∥AO,梯形AOBC的面积为10.
(1)求点A、B、C的坐标;
(2)求直线AC的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
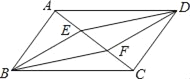
【题目】如图,在□ABCD中,E,F是对角线AC上的两点且AE=CF,在①BE=DF;②BE∥DF;③AB=DE;④四边形EBFD为平行四边形;⑤S△ADE=S△ABE;⑥AF=CE这些结论中正确的是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB⊥BC,AD∥BC,∠BCD=120°,BC=2,AD=DC.P为四边形ABCD边上的任意一点,当∠BPC=30°时,CP的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】回答下列问题:
(1)如图所示的甲、乙两个平面图形能折什么几何体?

(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为f,顶点个数为v,棱数为e,分别计算第(1)题中两个多面体的f+v﹣e的值?你发现什么规律?
(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com