
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌвЛДЮКЏЪ§![]() ЕФЭМЯѓЗжБ№гыxжсЁЂyжсЯрНЛгкЕуAЁЂBЃЌЧвгыОЙ§ЕуCЃЈ2ЃЌ0ЃЉЕФвЛДЮКЏЪ§y=kx+bЕФЭМЯѓЯрНЛгкЕуDЃЌЕуDЕФКсзјБъЮЊ4ЃЌжБЯпCDгыyжсЯрНЛгкЕуEЃЎ
ЕФЭМЯѓЗжБ№гыxжсЁЂyжсЯрНЛгкЕуAЁЂBЃЌЧвгыОЙ§ЕуCЃЈ2ЃЌ0ЃЉЕФвЛДЮКЏЪ§y=kx+bЕФЭМЯѓЯрНЛгкЕуDЃЌЕуDЕФКсзјБъЮЊ4ЃЌжБЯпCDгыyжсЯрНЛгкЕуEЃЎ
ЃЈ1ЃЉжБЯпCDЕФКЏЪ§БэДяЪНЮЊЁЁ ЁЁЃЛЃЈжБНгаДГіНсЙћЃЉ
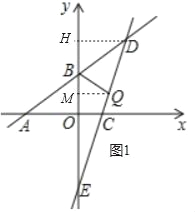
ЃЈ2ЃЉЕуQЮЊЯпЖЮDEЩЯЕФвЛИіЖЏЕуЃЌСЌНгBQЃЎ
ЂйШєжБЯпBQНЋЁїBDEЕФУцЛ§ЗжЮЊ1ЃК2СНВПЗжЃЌЪдЧѓЕуQЕФзјБъЃЛ
ЂкНЋЁїBQDбизХжБЯпBQЗелЃЌЪЙЕУЕуDЧЁКУТфдкжБЯпABЯТЗНЕФзјБъжсЩЯ,ЧыжБНгаДГіЕуQЕФзјБъ: .

ЁОД№АИЁПЃЈ1ЃЉy=3xЉ6ЃЛЃЈ2ЃЉЂйЃЈ![]() ЃЌЉ2ЃЉЛђЃЈ
ЃЌЉ2ЃЉЛђЃЈ![]() ЃЌ2ЃЉЃЛЂкДцдкЃЌЕуQЕФзјБъЮЊЃЈ3ЃЌ3ЃЉЛђЃЈ
ЃЌ2ЃЉЃЛЂкДцдкЃЌЕуQЕФзјБъЮЊЃЈ3ЃЌ3ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЧѓГіCЁЂDСНЕузјБъМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉЂйЗжСНжжЧщаЮSЁїBEQ=![]() SЁїBDEЛђSЁїBEQ=
SЁїBDEЛђSЁїBEQ=![]() SЁїBDEЗжБ№ЙЙНЈЗНГЬМДПЩЃЛ
SЁїBDEЗжБ№ЙЙНЈЗНГЬМДПЩЃЛ
ЂкЗжСНжжЧщаЮЃКЕБЕуDТфдкxе§АыжсЩЯЃЈМЧЮЊЕуD1ЃЉЪБЃЌШчЭМ2жаЃЛЕБЕуDТфдкyИКАыжсЩЯЃЈМЧЮЊЕуD2ЃЉЪБЃЌШчЭМ3жаЃЛЗжБ№ЧѓНтМДПЩ.
НтЃКЃЈ1ЃЉгЩЬтвтЃКDЃЈ4ЃЌ6ЃЉЃЌCЃЈ2ЃЌ0ЃЉЃЌ
ЩшжБЯпCDЕФНтЮіЪНЮЊy=kx+bЃЌ
дђга![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
ЁржБЯпCDЕФНтЮіЪНЮЊy=3xЉ6ЃЌ
ЙЪД№АИЮЊЃКy=3xЉ6ЃЛ
ЃЈ2ЃЉЂйЁпжБЯпBQНЋЁїBDEЕФУцЛ§ЗжЮЊ1ЃК2СНВПЗжЃЌ
ЁрSЁїBEQ=![]() SЁїBDEЛђSЁїBEQ=
SЁїBDEЛђSЁїBEQ=![]() SЁїBDEЃЌ
SЁїBDEЃЌ
дкy=![]() x+3жаЃЌЕБx=0ЪБЃЌy=3ЃЛЕБx=4ЪБЃЌy=6ЃЌ
x+3жаЃЌЕБx=0ЪБЃЌy=3ЃЛЕБx=4ЪБЃЌy=6ЃЌ
ЁрBЃЈ0ЃЌ3ЃЉЃЌDЃЈ4ЃЌ6ЃЉЃЎ
дкy=3xЉ6жаЃЌЕБx=0ЪБЃЌy=Љ6ЃЌ
ЁрEЃЈ0ЃЌЉ6ЃЉЃЌ
ЁрBE=9ЃЌ
ШчЭМ1жаЃЌЙ§ЕуDзїDHЁЭyжсгкЕуHЃЌдђDH=4ЃЌ
ЁрSЁїBDE=![]() BEDH=
BEDH=![]() ЁС9ЁС4=18ЃЌ
ЁС9ЁС4=18ЃЌ
ЁрSЁїBEQ=![]() ЁС18=6ЛђSЁїBEQ=
ЁС18=6ЛђSЁїBEQ=![]() ЁС18=12ЃЌ
ЁС18=12ЃЌ
ЩшQЃЈtЃЌ3tЉ6ЃЉЃЌгЩЬтвтжЊtЃО0ЃЌ
Й§ЕуQзїQMЁЭyжсгкЕуMЃЌдђQM=tЃЌ
Ёр![]() ЁС9ЁСt=6Лђ
ЁС9ЁСt=6Лђ![]() ЁС9ЁСt=12ЃЌ
ЁС9ЁСt=12ЃЌ
НтЕУt=![]() Лђ
Лђ![]() ЃЌ
ЃЌ
ЕБt=![]() ЪБЃЌ3tЉ6=Љ2ЃЌ
ЪБЃЌ3tЉ6=Љ2ЃЌ
ЕБt=![]() ЪБ3tЉ6=2ЃЌ
ЪБ3tЉ6=2ЃЌ
ЁрQЕФзјБъЮЊЃЈ![]() ЃЌЉ2ЃЉЛђЃЈ
ЃЌЉ2ЃЉЛђЃЈ![]() ЃЌ2ЃЉЃЛ
ЃЌ2ЃЉЃЛ
ЂкЕБЕуDТфдкxе§АыжсЩЯЃЈМЧЮЊЕуD1ЃЉЪБЃЌШчЭМ2жаЃЌ
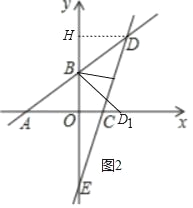
гЩЃЈ2ЃЉжЊBЃЈ0ЃЌ3ЃЉЃЌDЃЈ4ЃЌ6ЃЉЃЌ
ЁрBH=BO=3ЃЌ
гЩЗелЕУBD=BD1ЃЌ
дкЁїRtЁїDHBКЭRtЁїD1OBжаЃЌ
![]() ЃЌ
ЃЌ
ЁрRtЁїDHBЁеRtЁїD1OBЃЈHLЃЉЃЌ
ЁрЁЯDBH=ЁЯD1BOЃЌ
гЩЗелЕУЁЯDBQ=ЁЯD1BQЃЌ
ЁрЁЯHBQ=ЁЯOBQ=90ЁуЃЌ
ЁрBQЁЮxжсЃЌ
ЁрЕуQЕФзнзјБъЮЊ3ЃЌ
дкy=3xЉ6жаЃЌЕБy=3ЪБЃЌx=3ЃЌ
ЁрQЃЈ3ЃЌ3ЃЉЃЛ
ЕБЕуDТфдкyИКАыжсЩЯЃЈМЧЮЊЕуD2ЃЉЪБЃЌШчЭМ3жаЃЌ
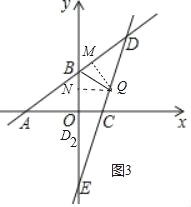
Й§ЕуQзїQMЁЭBDЃЌQNЁЭOBЃЌДЙзуЗжБ№ЮЊЕуMЁЂNЃЌ
гЩЗелЕУЁЯDBQ=ЁЯD2BQЃЌ
ЁрQM=QNЃЌ
гЩЃЈ2ЃЉжЊSЁїBDE=18ЃЌМДSЁїBQD+SЁїBQE=18ЃЌ
Ёр![]() BDQM+
BDQM+![]() BEQN=18ЃЌ
BEQN=18ЃЌ
гЩСНЕужЎМфЕФОрРыЙЋЪНЃЌЕУBD=![]() =5ЃЌ
=5ЃЌ
Ёр![]() ЁС5QN+
ЁС5QN+![]() ЁС9QN=18ЃЌ
ЁС9QN=18ЃЌ
НтЕУQN=![]() ЃЌ
ЃЌ
ЁрЕуQЕФКсзјБъЮЊ![]() ЃЌ
ЃЌ
дкy=3xЉ6жаЃЌЕБx=ЪБЃЌy=
![]() ЃЌ
ЃЌ
ЁрQЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
злКЯжЊЃЌЕуQЕФзјБъЮЊЃЈ3ЃЌ3ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
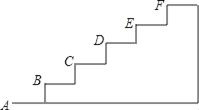
ЁОЬтФПЁПШчЭМЪЧФГЬЈНзЕФвЛВПЗжЃЌШчЙћAЕуЕФзјБъЮЊЃЈ0ЃЌ0ЃЉЃЌBЕуЕФзјБъЮЊЃЈ1ЃЌ1ЃЉЃЌ
ЃЈ1ЃЉЧыНЈСЂЪЪЕБЕФжБНЧзјБъЯЕЃЌВЂаДГіЦфгрИїЕуЕФзјБъЃЛ
ЃЈ2ЃЉШчЙћЬЈНзга10МЖЃЌЧыФуЧѓГіИУЬЈНзЕФГЄЖШКЭИпЖШЃЛ
ЃЈ3ЃЉШєет10МЖЬЈНзЕФПэЖШЖМЪЧ2mЃЌЕЅЮЛГЄЖШЮЊ1mЃЌЯжвЊНЋетаЉЬЈНзЦЬЩЯЕиЬКЃЌашвЊЖрЩйЦНЗНУзЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬГЁМЦЛЎЙКНј![]() ЁЂ
ЁЂ![]() СНжжаТаЭНкФмЬЈЕЦЙВ
СНжжаТаЭНкФмЬЈЕЦЙВ![]() еЕЃЌетСНжжЬЈЕЦЕФНјМлЁЂЪлМлШчБэЫљЪОЃК
еЕЃЌетСНжжЬЈЕЦЕФНјМлЁЂЪлМлШчБэЫљЪОЃК

ЃЈ![]() ЃЉШєЩЬГЁдЄМЦНјЛѕПюЮЊ
ЃЉШєЩЬГЁдЄМЦНјЛѕПюЮЊ![]() дЊЃЌдђетСНжжЬЈЕЦИїЙКНјЖрЩйеЕЃП
дЊЃЌдђетСНжжЬЈЕЦИїЙКНјЖрЩйеЕЃП
ЃЈ![]() ЃЉШєЩЬГЁЙцЖЈ
ЃЉШєЩЬГЁЙцЖЈ![]() аЭЬЈЕЦЕФНјЛѕЪ§СПВЛГЌЙ§
аЭЬЈЕЦЕФНјЛѕЪ§СПВЛГЌЙ§![]() аЭЬЈЕЦЪ§СПЕФ
аЭЬЈЕЦЪ§СПЕФ![]() БЖЃЌгІдѕбљНјЛѕВХФмЪЙЩЬГЁдкЯњЪлЭъетХњЬЈЕЦЪБЛёРћзюЖрЃПДЫЪБРћШѓЮЊЖрЩйдЊЃП
БЖЃЌгІдѕбљНјЛѕВХФмЪЙЩЬГЁдкЯњЪлЭъетХњЬЈЕЦЪБЛёРћзюЖрЃПДЫЪБРћШѓЮЊЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГбЇаЃПЊеЙПЮЭтЬхг§ЛюЖЏЃЌОіЖЈПЊеЙЃКРКЧђЁЂЦЙХвЧђЁЂЬпыІзгЁЂХмВНЫФжжЛюЖЏЯюФП.ЮЊСЫНтбЇЩњзюЯВЛЖФФвЛжжЛюЖЏЯюФПЃЈУПШЫжЛбЁШЁвЛжжЃЉ.ЫцЛњГщШЁСЫВПЗжбЇЩњНјааЕїВщЃЌВЂНЋЕїВщНсЙћЛцГЩШчЯТЭГМЦЭМЃЌЧыФуНсКЯЭМжааХЯЂНтД№ЯТСаЮЪЬт.
ЃЈ1ЃЉбљБОжазюЯВЛЖРКЧђЯюФПЕФШЫЪ§ЫљеМЕФАйЗжБШЮЊ ЃЌЦфЫљдкЩШаЮЭГМЦЭМжаЖдгІЕФдВаФНЧЖШЪ§ЪЧ ЖШЃЛ
ЃЈ2ЃЉЧыАбЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉШєИУаЃгабЇЩњ1000ШЫЃЌЧыИљОнбљБОЙРМЦШЋаЃзюЯВЛЖЬпыІзгЕФбЇЩњШЫЪ§дМЪЧЖрЩйЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
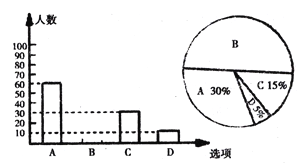
ЁОЬтФПЁПЮЊСЫНтбЇЩњВЮМгЬхг§ЛюЖЏЕФЧщПіЃЌбЇаЃЖдбЇЩњНјааЫцЛњГщбљЕїВщЃЌЦфжавЛИіЮЪЬтЪЧЁАФуЦНОљУПЬьВЮМгЬхг§ЛюЖЏЕФЪБМфЪЧЖрЩйЃПЁБЙВга4ИібЁЬтЃЎ
AЃЎ1.5аЁЪБвдЩЯЁЁЁЁЁЁЁЁBЃЎ1ЁЋ1.5аЁЪБЁЁЁЁЁЁЁЁCЃЎ0.5ЁЋ1аЁЪБЁЁЁЁЁЁЁЁDЃЎ0.5аЁЪБвдЯТ
ЧыФуИљОнЭГМЦЭМЬсЙЉЕФаХЯЂЃЌНтД№вдЯТЮЪЬтЃК
ЃЈ1ЃЉБОДЮвЛЙВЕїВщСЫЖрЩйУћбЇЩњЃП
ЃЈ2ЃЉНЋЬѕаЮЭГМЦЭМбЁЯюBВЙГфЭъећЃЛ
ЃЈ3ЃЉШєИУаЃга3000УћбЇЩњЃЌФуЙРМЦШЋаЃПЩФмгаЖрЩйУћбЇЩњЦНОљУПЬьВЮМгЬхг§ЛюЖЏЕФЪБМфдк0.5аЁЪБвдЯТЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌABЮЊЁбOЕФжБОЖЃЌЁбOгыDCЯрЧагкЕуEЃЌгыADЯрНЛгкЕуFЃЌвбжЊAB=12ЃЌЁЯC=60ЁуЃЌдђ ![]() ЕФГЄЮЊЃЈ ЃЉ
ЕФГЄЮЊЃЈ ЃЉ 
A.![]()
B.![]()
C.Іа
D.2Іа
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЋдАЕФУХЦБУПеХ10дЊЃЌЮЊСЫЮќв§ИќЖрЕФгЮПЭЃЌИУЙЋдАЙмРэГ§БЃСєдРДЕФЪлЦБЗНЗЈЭтЃЌЛЙЭЦГіСЫвЛжжЁАЙКТђФъПЈЁБЕФгХЛнЗНЗЈЃЌФъПЈЗжЮЊAЁЂBЁЂCШ§жжЃКAПЈУПеХ120дЊЃЌГжПЈНјШыВЛгУдйТђУХЦБЃЛBПЈУПеХ60дЊЃЌГжПЈНјШыЙЋдАашвЊдйТђУХЦБЃЌУПеХ2дЊЃЛCПЈУПеХ30дЊЃЌГжЦБНјШыЙЋдАЪБЃЌЙКТђУПеХ4дЊЕФУХЦБЃЎ
ЃЈ1ЃЉШчЙћФужЛбЁдёвЛжжЙКТђУХЦБЕФЗНЪНЃЌВЂЧвФуМЦЛЎдквЛФъжагУ100дЊЛЈдкШЅИУЙЋдАЭцЕФУХЦБЩЯЃЌЧыЮЪФФжжЙКЦБЗНЪНПЩЪЙФуНјШыИУЙЋдАЕФДЮЪ§зюЖрЃП
ЃЈ2ЃЉЧѓвЛФъжаНјШыИУЙЋдАжСЩйЖрЩйДЮЃЌЙКТђAРрФъЦББШНЯКЯЫуЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
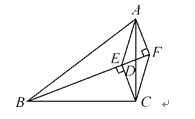
ЁОЬтФПЁПШчЭМЫљЪОЃЌBDЪЧЁїABCЕФжаЯпЃЌCEЁЭBDгкЕуEЃЌAFЁЭBDЃЌНЛBDЕФбгГЄЯпгкЕуF.
(1)ЪдЬНЫїBEЃЌBFКЭBDШ§епжЎМфЕФЪ§СПЙиЯЕЃЌВЂМгвджЄУїЃЛ
(2)СЌНгAEЃЌCFЃЌЧѓжЄЃКAEЁЮCF.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧФГЭэБЈЁААйаеШШЯпЁБвЛжмФкНгЕНШШЯпЕчЛАЕФЭГМЦЭМЃЌЦфжагаЙиЛЗОГБЃЛЄЮЪЬтЕФЕчЛАзюЖрЃЌЙВ70ИіЃЌЧыЛиД№ЯТСаЮЪЬтЃК

ЃЈ1ЃЉБОжмЁААйаеШШЯпЁБЙВНгЕНШШЯпЕчЛАЖрЩйИіЃП
ЃЈ2ЃЉгаЙиЕРТЗНЛЭЈЮЪЬтЕФЕчЛАЖрЩйИіЃП
ЃЈ3ЃЉМЦЫуЦфЫћИїРрЕчЛАЕФИіЪ§.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com