
����Ŀ����ͼ�٣��ڳ�����ABCD�У�AB��10 cm��BC��8 cm����P��A��������A��B��C��D·���˶�����Dֹͣ����P���ٶ�Ϊÿ��1 cm��a��ʱ��P���ٶȱ�Ϊÿ��bcm��ͼ���ǵ�P����x�����APD�����S1��cm2����y���룩�ĺ�����ϵͼ��
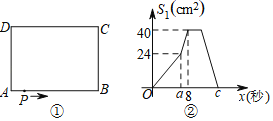
��1������ͼ�����ṩ����Ϣ��a���� ��b���� ��c���� ��
��2����P�������룬��APD�����S1�dz�����ABCD������ķ�֮һ��
���𰸡���1��a��6��b��2��c��17����2����P������5���14.5�룬��APD�����S1�dz�����ABCD������ķ�֮һ.
��������
��1���ɸ��ݺ���ͼ��ֶ����������ε������ʽ�׳��Ըߣ���Ϊ8cmһ��������ʱ��ı仯���仯�����a��b��cΪ����ʱ��ĺͣ�
��2���ɷ������������ɵã���P��AB�е��CD�е�ʱ����APD�����S1�dz�����ABCD������ķ�֮һ��
�⣺��1��������ͼ���֪��
��0��x��aʱ��S1��![]() ��8a��24 ����a��6
��8a��24 ����a��6
��a��x��8ʱ��S1��![]() ��8��[6��1+b��8��6��]��40 ����b��2
��8��[6��1+b��8��6��]��40 ����b��2
��8��x��cʱ��
�ٵ���P��B���˶���C��������APD�����S1��![]() ��8��10��40��cm2��һ��������ʱ���ǣ�8��2��4���룩��
��8��10��40��cm2��һ��������ʱ���ǣ�8��2��4���룩��
�ڵ���P��C���˶���D�㣺����ʱ���ǣ�10��2��5���룩��
����c��8+4+5��17���룩��
�ʴ�Ϊ��a��6��b��2��c��17��
��2���߳�����ABCD����ǣ�10��8��80��cm2��
�൱0��x��aʱ��![]() ��8x��80��
��8x��80��![]() ����x��5��
����x��5��
��12��x��17ʱ��![]() ��8��2��17��x����80��
��8��2��17��x����80��![]() ����x��14.5��
����x��14.5��
���P������5���14��5�룬��APD�����S1�dz�����ABCD������ķ�֮һ��


 �ο�������ϵ�д�
�ο�������ϵ�д� ������ѧ��ʱ��ҵϵ�д�
������ѧ��ʱ��ҵϵ�д� ���������ʱ��ѵϵ�д�
���������ʱ��ѵϵ�д� �㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
�㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ���˽���и��꼶ѧ��ÿ���ƽ��˯��ʱ�䣨��λ��h����ȷ��1 h�������������˲���ѧ�������õõ������ݻ���������������������ͳ��ͼ��
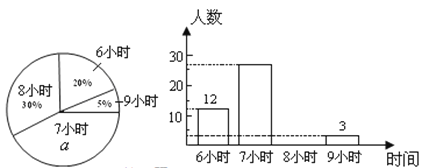
�������ͼ���ṩ����Ϣ���ش��������⣺
��1���������ͳ��ͼ�аٷ���![]() ��ֵΪ_______��������ѧ������Ϊ______��
��ֵΪ_______��������ѧ������Ϊ______��
��2�����ƽ��˯��ʱ��Ϊ8Сʱ������������ȫ����ͼ��
��3������ⲿ��ѧ����ƽ��˯��ʱ���ƽ������
��4�������У����ѧ��1200�����������˯�߲��㣨����8Сʱ����ѧ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
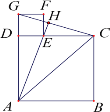
����Ŀ����ͼ����֪�ı���![]() ���ı���
���ı���![]() Ϊ�����Σ���
Ϊ�����Σ���![]() ���߶�
���߶�![]() �ϣ���
�ϣ���![]() ��ͬһֱ���ϣ�����
��ͬһֱ���ϣ�����![]() �����ӳ�
�����ӳ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
��1����֤��![]() ��
��
��2����![]() ��
��![]() �����߶�
�����߶�![]() �ij���
�ij���
��3����![]() ��
��![]() ������H���߶�GC���е�ʱ����
������H���߶�GC���е�ʱ����![]() ��
��![]() ����ʲô���Ĺ�ϵʽ.
����ʲô���Ĺ�ϵʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ������л�����ѧ���ݽ������У���λ��ί�ֱ���ס�����λѡ�ֵ��������£��ף�8��7��9��8��8���ң�7��9��6��9��9��������˵���д�����ǣ�������
A. �÷ֵķ�����ҵ÷ֵķ���СB. �÷ֵ�������8���ҵ÷ֵ�������9
C. �ס��ҵ÷ֵ�ƽ��������8D. �÷ֵ���λ����9���ҵ÷ֵ���λ����6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������˵ڶ����������۳������Ķ���ȫ���Ķ����Ϊ�˽�����ÿ����Ķ�ʱ������������ȡ�˲���������е��飮���ݵ��������������в�������Ƶ���ֲ�����
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
(1) ��ȫ����
(2) ��ÿ���Ķ�ʱ�䲻���� ![]() �������Ϊ���Ķ�����������������Լ��
�������Ϊ���Ķ�����������������Լ�� ![]() ���ˣ�����������ܳ�Ϊ���Ķ���������������Լ�ж������ˣ�
���ˣ�����������ܳ�Ϊ���Ķ���������������Լ�ж������ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
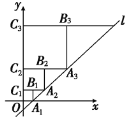
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l��![]() ��x�ύ�ڵ�A1����ͼ��ʾ������������A1B1C1O��
��x�ύ�ڵ�A1����ͼ��ʾ������������A1B1C1O��
������A2B2C2C1������������![]() ��ʹ�õ�A1��A2��A3������ֱ��l�ϣ���C1��C2��C3����
��ʹ�õ�A1��A2��A3������ֱ��l�ϣ���C1��C2��C3����
��y���������ϣ����![]() ��������_______________________.
��������_______________________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����г�����ij���������³����������������ǰϦ������һ��Ʒ�����ӣ�ÿ�н�����40Ԫ�����й涨ÿ���ۼ۲�������45Ԫ�������������۾��鷢�֣����ۼ۶�Ϊÿ��45Ԫʱ��ÿ���������700�У�ÿ���ۼ�ÿ���1Ԫ��ÿ��Ҫ������20�У�
��1�������ÿ���������y���У���ÿ���ۼ�x��Ԫ��֮��ĺ�����ϵʽ��
��2����ÿ���ۼ۶�Ϊ����Ԫʱ��ÿ�����۵�����P��Ԫ�������������Ƕ��٣�
��3��Ϊ�ȶ���ۣ��йع������������������ӵ�ÿ���ۼ۲��ø���58Ԫ�����������Ҫÿ���ò�����6000Ԫ��������ô����ÿ�������������Ӷ��ٺУ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
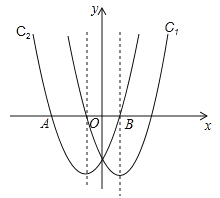
����Ŀ����ͬһֱ������ϵ�У�������y=ax2��2x��3��������y=x2+mx+n����y��Գƣ�C2��x�ύ��A��B���㣬���е�A�ڵ�B����࣮
��1����������C1��C2�ĺ�������ʽ��
��2����A��B��������ꣻ
��3����������C1���Ƿ����һ��P����������C2���Ƿ����һ��Q��ʹ����ABΪ�ߣ�����A��B��P��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ������ڣ����P��Q��������ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
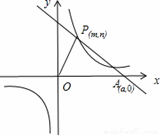
����Ŀ����֪��O������ԭ�㣬P��m��n��(m��0)�Ǻ���y �� ![]() (k��0)�ϵĵ㣬����P��ֱ��PA��OP��P��ֱ��PA��x��������ύ�ڵ�A��a��0��(a��m). ����OPA�����Ϊs����s��1��
(k��0)�ϵĵ㣬����P��ֱ��PA��OP��P��ֱ��PA��x��������ύ�ڵ�A��a��0��(a��m). ����OPA�����Ϊs����s��1��![]() .
.
��1����n��1ʱ�����A�����ꣻ
��2����OP��AP����k��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com