练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在“爱我中华”中学生演讲比赛中，五位评委分别给甲、乙两位选手的评分如下：甲：8，7，9，8，8；乙：7，9，6，9，9，则下列说法中错误的是（　　）

    A. 甲得分的方差比乙得分的方差小B. 甲得分的众数是8，乙得分的众数是9

    C. 甲、乙得分的平均数都是8D. 甲得分的中位数是9，乙得分的中位数是6

    【答案】D

    【解析】

    分别求出甲、乙的平均数、方差、众数、中位数即可逐一判断．

    解：甲得分的平均数为：（8+7+9+8+8）÷5＝8，乙得分的平均数为：（7+9+6+9+9）÷5＝8；

    甲得分的方差为：×[（8﹣8）2+（7﹣8）2+（9﹣8）2+（8﹣8）2+（8﹣8）2]＝×2＝0.4，

    乙得分的方差为：×[（7﹣8）2+（9﹣8）2+（6﹣8）2+（9﹣8）2+（9﹣8）2]＝×8＝1.6，

    故A、C都正确；

    甲得分次数最多是8分，即众数为8分，乙得分最多的是9分，即众数为9分，故B正确；

    C、∵甲得分从小到大排列为：7、8、8、8、9，∴甲的中位数是8分；

    ∵乙得分从小到大排列为：6、7、9、9、9，∴乙的中位数是9分；故D错误；

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC的三个顶点分别为， ， .若反比例函数在第一象限内的图象与△ABC有公共点，则k的取值范围是__________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在正方形ABCD中，动点E，F分别从D，C两点同时出发，以相同的速度在直线DC，CB上移动.

    （1）如图1，当点E在边DC上自D向C移动，同时点F在边CB上自C向B移动时，连接AE和DF交于点P，请你写出AE与DF的数量关系和位置关系，并说明理；

    （2）如图2，当E，F分别在边CD，BC的延长线上移动时，连接AE，DF，（1）中的结论还成立吗？（请你直接回答“是”或“否”，不需证明）；连接AC，求△ACE为等腰三角形时CE：CD的值；

    （3）如图3，当E，F分别在直线DC，CB上移动时，连接AE和DF交于点P，由于点E，F的移动，使得点P也随之运动，请你画出点P运动路径的草图.若AD=2，试求出线段CP的最大值.

    图1 图2 图3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校就“遇见路人摔倒后如何处理”的问题，随机抽取该校部分学生进行问卷调查，图1和图2是整理数据后绘制的两幅不完整的统计图. 请根据图中提供的信息，解答下列问题：

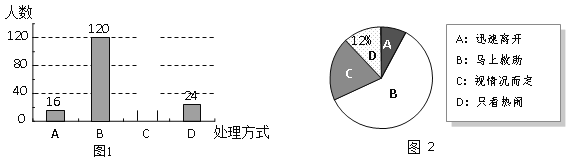
    （1）该校随机抽查了 名学生？请将图1补充完整；

    （2）在图2中，“视情况而定”部分所占的圆心角是 度；

    （3）在这次调查中，甲、乙、丙、丁四名学生都选择“马上救助”，现准备从这四人中随机抽取两人进行座谈，试用列表或树形图的方法求抽取的两人恰好是甲和乙的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）在△ABC中，∠ACB＝90°，AC＝BC，直线MN经过点C，AD⊥MN于点D，BE⊥MN于点E，当直线MN旋转到图1的位置时，求证：DE＝AD+BE；

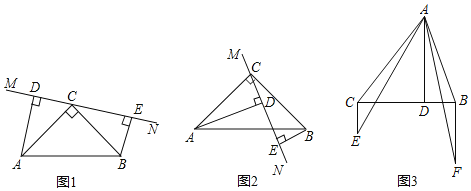
    （2）在（1）的条件下，当直线MN旋转到图2的位置时，猜想线段AD，DE，BE的数量关系，并证明你的猜想；

    （3）如图3，在△ABC中，AD⊥BC于D，AD＝BC，BF⊥BC于B，BF＝CD，CE⊥BC于C，CE＝BD，求证：∠EAF+∠BAC＝90°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】八年 2 班组织了一次经典诵读比赛，甲乙两组各 10 人的比赛成绩如下表（10 分制）：

    甲

    7

    8

    9

    7

    10

    10

    9

    10

    10

    10

    乙

    10

    8

    7

    9

    8

    10

    10

    9

    10

    9

    （Ⅰ）甲组数据的中位数是 ，乙组数据的众数是 ；

    （Ⅱ）计算乙组数据的平均数和方差；

    （Ⅲ）已知甲组数据的方差是 1.4 分，则成绩较为整齐的是 。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，在长方形ABCD中，AB＝10 cm，BC＝8 cm，点P从A出发，沿A、B、C、D路线运动，到D停止，点P的速度为每秒1 cm，a秒时点P的速度变为每秒bcm，图②是点P出发x秒后，△APD的面积S1（cm2）与y（秒）的函数关系图象：

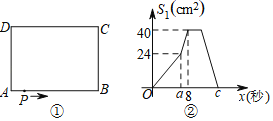
    （1）根据图②中提供的信息，a＝　 ，b＝　 ，c＝　 ．

    （2）点P出发后几秒，△APD的面积S1是长方形ABCD面积的四分之一？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，AC与BD相交于点O，∠BAD＝90°，BO＝DO，那么添加下列一个条件后，仍不能判定四边形ABCD是矩形的是(　　)

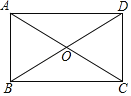
    A. ∠ABC＝90°B. ∠BCD＝90°C. AB＝CDD. AB∥CD

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】历史上对勾股定理的一种证法采用了如图所示图形，其中两个全等的直角三角形边AE，EB在一条直线上．证明中用到的面积相等关系是 ( )

    A. S△EDA=S△CEB

    B. S△EDA +S△CEB=S△CDB

    C. S四边形CDAE= S四边形CDEB

    D. S△EDA+S△CDE+S△CEB= S四边形ABCD

    查看答案和解析>>

    同步练习册答案