
【题目】(1)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,AD⊥MN于点D,BE⊥MN于点E,当直线MN旋转到图1的位置时,求证:DE=AD+BE;
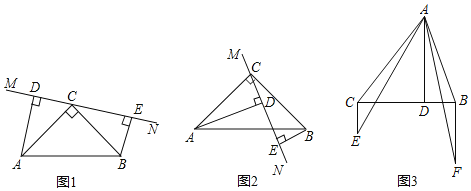
(2)在(1)的条件下,当直线MN旋转到图2的位置时,猜想线段AD,DE,BE的数量关系,并证明你的猜想;
(3)如图3,在△ABC中,AD⊥BC于D,AD=BC,BF⊥BC于B,BF=CD,CE⊥BC于C,CE=BD,求证:∠EAF+∠BAC=90°.
【答案】(1)见解析;(2)DE=AD﹣BE,证明见解析;(3)见解析.
【解析】
(1)由已知条件可推出∠ACD=∠CBE,继而可证明△ADC≌△CEB,利用全等三角形的性质可证明结论;
(2)与(1)证法类似,可推出∠ACD=∠CBE,证明△ADC≌△CEB,得出AD=CE,DC=BE,继而得出结论;
(3)连接CF、BE,可证明△ADC≌△CBF,进一步推出△ACF为等腰直角三角形,同理可推出△ABE为等腰直角三角形,从而可得出结论.
解:(1)证明:∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
而AD⊥MN于D,BE⊥MN于E,
∴∠ADC=∠CEB=90°,
∴∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,
在△ADC和△CEB中, ,
,
∴△ADC≌△CEB(AAS),
∴AD=CE,DC=BE,
∴DE=DC+CE=BE+AD;
(2)DE=AD﹣BE,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
而AD⊥MN于D,BE⊥MN于E,
∴∠ADC=∠CEB=90°,
∴∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,
在△ADC和△CEB中, ,
,
∴△ADC≌△CEB(AAS),
∴AD=CE,DC=BE,
∴DE=CE﹣CD=AD﹣BE;
(3)如图3,连接CF、BE,
AD⊥BC于D,BF⊥BC于B,
∴∠ADC=∠CBF=90°,
在△ADC和△CBF中,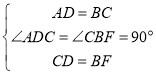 ,
,
∵△ADC≌△CBF(SAS),
∴∠CAD=∠FCB,AC=CF;
∴∠ACF=∠FCB+∠ACD=∠CAD+∠ACD=∠ADC=90°
∴△ACF为等腰直角三角形.
∴∠CAF=45°,
同理:△ABE为等腰直角三角形.
∴∠EAB=45°,
∴∠EAF+∠BAC=∠CAF+∠EAB=90°.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连接CF,以下结论:①△ABF≌△CBF;②点E到AB的距离是2![]() ;③tan∠DCF=
;③tan∠DCF=![]() ;④△ABF的面积为
;④△ABF的面积为![]() .其中一定成立的有几个( )
.其中一定成立的有几个( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节吃粽子是中华民族的传统习惯.农历五月初五早晨,小王的妈妈用不透明袋子装着一些粽子(粽子除食材不同外,其他一切相同),其中糯米粽两个,还有一些薯粉粽,现小王从中任意拿出一个是糯米粽的概率为![]() .
.
(1)求袋子中薯粉粽的个数;
(2)小王第一次任意拿出一个粽子(不放回),第二次再拿出一个粽子,请你用树形图或列表法,求小王两次拿到的都是薯粉粽的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
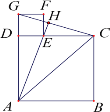
【题目】如图,已知四边形![]() 和四边形
和四边形![]() 为正方形,点
为正方形,点![]() 在线段
在线段![]() 上,点
上,点![]() 在同一直线上,连接
在同一直线上,连接![]() ,并延长
,并延长![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() .
.
(2)若![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
(3)设![]() ,
,![]() ,当点H是线段GC的中点时,则
,当点H是线段GC的中点时,则![]() 与
与![]() 满足什么样的关系式.
满足什么样的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 一个游戏的中奖概率是![]() ,则做10次这样的游戏一定会中奖
,则做10次这样的游戏一定会中奖
B. 为了解全国中学生的心理健康情况,应该采用普查的方式
C. 一组数据6,8,7,8,8,9,10的众数和中位数都是8
D. 若甲组数据的方差![]() ,乙组数据的方差
,乙组数据的方差![]() ,则乙组数据比甲组数据稳定
,则乙组数据比甲组数据稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“爱我中华”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:甲:8,7,9,8,8;乙:7,9,6,9,9,则下列说法中错误的是( )
A. 甲得分的方差比乙得分的方差小B. 甲得分的众数是8,乙得分的众数是9
C. 甲、乙得分的平均数都是8D. 甲得分的中位数是9,乙得分的中位数是6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市启动了第二届“美丽港城美在阅读”全民阅读活动.为了解市民每天的阅读时间情况,随机抽取了部分市民进行调查.根据调查结果绘制如下尚不完整的频数分布表:
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
(1) 补全表格;
(2) 将每天阅读时间不低于 ![]() 的市民称为“阅读爱好者”.若我市约有
的市民称为“阅读爱好者”.若我市约有 ![]() 万人,请估计我市能称为“阅读爱好者”的市民约有多少万人?
万人,请估计我市能称为“阅读爱好者”的市民约有多少万人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于58元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售粽子多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
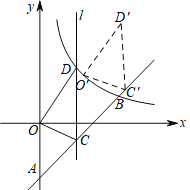
【题目】如图,一次函数y=kx-4(k≠0)的图象与y轴交于点A,与反比例函数y=![]() (x>0)的图象交于点B(6,b).
(x>0)的图象交于点B(6,b).
(1)b=__________;k=__________.
(2)点C是直线AB上的动点(与点A,B不重合),过点C且平行于y轴的直线l交这个反比例函数的图象于点D,当点C的横坐标为3时,得△OCD,现将△OCD沿射线AB方向平移一定的距离(如图),得到△O′C′D′,若点O的对应点O′落在该反比例函数图象上,求点O′,D′的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com