
����Ŀ����ͼ��һ�κ���y��kx��4��k��0����ͼ����y�ύ�ڵ�A���뷴��������y��![]() ��x��0����ͼ���ڵ�B��6��b����
��x��0����ͼ���ڵ�B��6��b����
��1��b��__________��k��__________��
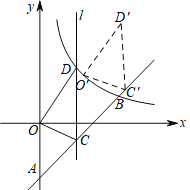
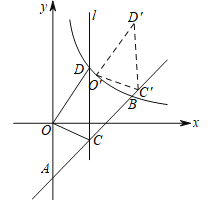
��2����C��ֱ��AB�ϵĶ��㣨���A��B���غϣ�������C��ƽ����y���ֱ��l�����������������ͼ���ڵ�D������C�ĺ�����Ϊ3ʱ������OCD���ֽ���OCD������AB����ƽ��һ���ľ��루��ͼ�����õ���O��C��D��������O�Ķ�Ӧ��O�����ڸ÷���������ͼ���ϣ����O����D�������꣮
���𰸡� ��1��2�� 1����2��![]() ,
, ![]() .
.
�������������������1����B��6��b������![]() ���ɵ�b��ֵ���ѵ�B���������һ�κ�������ʽ�����ɵõ�k��ֵ��
���ɵ�b��ֵ���ѵ�B���������һ�κ�������ʽ�����ɵõ�k��ֵ��
��2���ȸ��ݵ�C�ĺ�����Ϊ3����õ�C��D�����꣬��O'��a�� ![]() ������C'��a+3��
������C'��a+3�� ![]() ��1�������ݵ�C'��ֱ��y=x��4�ϣ��ɵ÷���
��1�������ݵ�C'��ֱ��y=x��4�ϣ��ɵ÷���![]() ��1=a+3��4�������õ�a��ֵ�������ó���O����D�������꣮
��1=a+3��4�������õ�a��ֵ�������ó���O����D�������꣮
����������⣺��1������B�ڷ���������![]() ��x��0����ͼ���ϣ���B��6��b������
��x��0����ͼ���ϣ���B��6��b������![]() ����b=2����B��6��2��������B��ֱ��y=kx��4�ϣ���2=6k��4�����k��1���ʴ�Ϊ��2��1��
����b=2����B��6��2��������B��ֱ��y=kx��4�ϣ���2=6k��4�����k��1���ʴ�Ϊ��2��1��
��2������C�ĺ�����Ϊ3����x=3����y=x��4����y=��1����C��3����1������CD��y�ᣬ����D�ĺ�����Ϊ3����x=3����![]() ���ɵ�y=4����D��3��4����
���ɵ�y=4����D��3��4����
��ƽ�ƿɵã���OCD�ա�O'C'D'����O'��a�� ![]() ������C'��a+3��
������C'��a+3�� ![]() ��1��������C'��ֱ��y=x��4�ϣ���
��1��������C'��ֱ��y=x��4�ϣ���![]() ��1=a+3��4����
��1=a+3��4����![]() =a����a��0����a=
=a����a��0����a=![]() ����O'��
����O'��![]() ��
�� ![]() ������D'��
������D'��![]() +3��
+3�� ![]() +4����
+4����


 ����ѵ�����⿼ϵ�д�
����ѵ�����⿼ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�
��������5�멁2���Ե�����֮��ľ��룺|5������2��|=7��
�������ϩ�2��3���Ե�����֮��ľ��룺|��2��3|=5��
�������ϩ�8�멁5���Ե�����֮��ľ��룺|����8��������5��|=3
�������ϵ�A��B�ֱ��ʾ��a��b����A��B����֮��ľ���AB=|a��b|=|b��a|
�ش��������⣺
��1�������ϱ�ʾ��2�ͩ�5������֮��ľ�����_____��
�����ϱ�ʾ��x��3������֮��ľ����ʾΪ_____��
�����ϱ�ʾ��_____��_____������֮��ľ����ʾΪ|x+2|����
��2�����꼶�о���ѧϰС������ѧ��ʦָ���£���ʽ��|x+2|+|x��3|����̽����
�������ڲݸ�ֽ�ϻ������ᣬ����ʾ��x�ĵ��ک�2��3֮���ƶ�ʱ��|x��3|+|x+2|��ֵ����һ���̶���ֵΪ��_____��
�������ڲݸ�ֽ�ϻ������ᣬҪʹ|x��3|+|x+2|=7�������ϱ�ʾ�����x=_____��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ����������
����������![]() ��
��![]()
��1����![]() ��
��![]() ��ֵ��
��ֵ��
��2���ú���![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() ��
��
��3����![]() �Dz���
�Dz�С��![]() �ĸ�������
�ĸ�������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
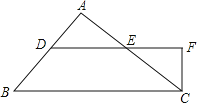
����Ŀ����֪����ͼ������ABC�У���A��90������D��E�ֱ���AB��AC�ϣ�DE��BC��CF��DE���ӳ��ߴ�ֱ������ΪF��
��1)��֤����B����ECF ��
��2������B��55��������CED�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
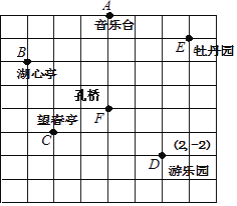
����Ŀ����ϼ�Ͱְ֡����赽�������棬�ص��Һ�������ƽ��ֱ������ϵ�����˹��ľ�����ͼ����ͼ��ʾ����������������ͼ�б��ԭ���x�ᣮy�ᣮֻ֪������D������Ϊ��2����2�������������������ϵ����д����������������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ1����λ���ȵ�С��������ɵ���������
��1����![]() ƽ����
ƽ����![]() ��λ�ã�ʹ��
��λ�ã�ʹ��![]() ��
��![]() ��Ӧ���õ�
��Ӧ���õ�![]() ��
��
��2��ͼ�п�����ĸ��ʾ�����߶�![]() ƽ������ȵ��߶�����Щ��
ƽ������ȵ��߶�����Щ��
��3�����ı���![]() �������
�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ��
��![]() Ϊ����ԭ�㣬
Ϊ����ԭ�㣬![]() ������Ϊ
������Ϊ![]() ��
��![]() ����
����![]() ����������ϣ�
����������ϣ�![]() ����
����![]() ����������ϣ�
����������ϣ�![]() ���߶�
���߶�![]() �ϵĶ��㣬��
�ϵĶ��㣬��![]() ����֪��
����֪��![]() �ڵ�һ��������ֱ��
�ڵ�һ��������ֱ��![]() ��һ�㣬��
��һ�㣬��![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�
��![]() �����
�����![]() �����겢д��������̣�
�����겢д��������̣�
��![]() ��ֱ��
��ֱ��![]() ����ƽ��
����ƽ��![]() ����λ���ڸ�ֱ�����Ƿ���ڵ�
����λ���ڸ�ֱ�����Ƿ���ڵ�![]() ��ʹ
��ʹ![]() �ǵ���ֱ����������
�ǵ���ֱ����������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
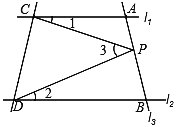
����Ŀ����ͼ����ֱ֪��l1��l2����l3��l1��l2�ֱ���A��B���㣬��P��ֱ��AB��.
��1����˵����1����2����3֮��Ĺ�ϵʽ����Ҫ��д���������̣�
��2�������P��A��B����֮�䣨��P��A��B���غϣ��˶�ʱ����̽����1����2����3֮��Ĺ�ϵ�Ƿ����仯����ֻ�ش�
��3�������P��A��B������ࣨ��P��A��B���غϣ��˶�ʱ����̽����1����2����3֮��Ĺ�ϵ.��Ҫ��д���������̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����A������CE�ϣ���C=��D��
��1����ͼ1����AC��BD����֤��AD��BC��
��2����ͼ2������BAC=��BAD��BD��BC����̽����DAE����C��������ϵ��д�����̽�����ۣ�������֤����
��3����ͼ3���ڣ�2���������£�����D��DF��BC�������ڵ�F������DFE=8��DAEʱ������BAD�Ķ�����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com