
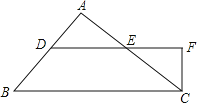
【题目】已知:如图,在△ABC中,∠A=90°,点D、E分别在AB、AC上,DE∥BC,CF与DE的延长线垂直,垂足为F.
(1)求证:∠B=∠ECF ;
(2)若∠B=55°,求∠CED的度数.
【答案】(1)见解析;(2) 145°
【解析】试题分析:(1)先由DE∥BC得出∠B=∠ADE,再根据∠A=90°得出∠ADE+∠AED=90°.由∠F=90°可知∠ECF+∠CEF=90°.由对顶角相等可知∠AED=∠CEF,故∠ADE=∠ECF,由此可得出∠B=∠ECF;
(2)由(1)可知∠B=∠ECF=55°,故∠CED=∠F+∠ECF=90°+55°=145°.
证明:(1)∵DE∥BC,
∴∠B=∠ADE.
∵∠A=90°,
∴∠ADE+∠AED=90°.
∵∠F=90°,
∴∠ECF+∠CEF=90°.
∵∠AED=∠CEF,
∴∠ADE=∠ECF,
∴∠B=∠ECF;
(2)∵由(1)可知∠B=∠ECF=55°,
∴∠CED=∠F+∠ECF=90°+55°=145°.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在某住房小区的建设中,为了提高业主的宜居环境,小区准备在一个长为(4a+3b)米,宽为(2a+3b)米的长方形草坪上修建两条宽为b米的通道.
(1)通道的面积是多少平方米?
(2)剩余草坪的面积是多少平方米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=50°,∠ACB=60°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,连接AD,下列结论中不正确的是( )

A. ∠BAC=70° B. ∠DOC=90° C. ∠BDC=35° D. ∠DAC=55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠ABC=![]() ,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )
,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )

A. 1个
B. 2个
C. 3个
D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx-4(k≠0)的图象与y轴交于点A,与反比例函数y=![]() (x>0)的图象交于点B(6,b).
(x>0)的图象交于点B(6,b).
(1)b=__________;k=__________.
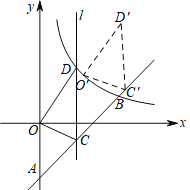
(2)点C是直线AB上的动点(与点A,B不重合),过点C且平行于y轴的直线l交这个反比例函数的图象于点D,当点C的横坐标为3时,得△OCD,现将△OCD沿射线AB方向平移一定的距离(如图),得到△O′C′D′,若点O的对应点O′落在该反比例函数图象上,求点O′,D′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
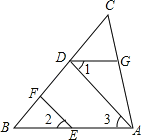
【题目】如图,已知点D、F、E、G都在△ABC的边上,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.(请在下面的空格处填写理由或数学式)
解:∵EF∥AD,(已知)
∴∠2= ( )
∵∠1=∠2,(已知)
∴∠1= (等量代换)
∴ ∥ ,( )
∴∠AGD+ =180°,(两直线平行,同旁内角互补)
∵∠CAB=70° ,(已知)
∴∠AGD= (等式性质)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com