
����Ŀ����������ABCD�У�����E��F�ֱ��D��C����ͬʱ����������ͬ���ٶ���ֱ��DC��CB���ƶ�.
��1����ͼ1������E�ڱ�DC����D��C�ƶ���ͬʱ��F�ڱ�CB����C��B�ƶ�ʱ������AE��DF���ڵ�P������д��AE��DF��������ϵ��λ�ù�ϵ����˵������
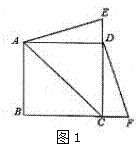
��2����ͼ2����E��F�ֱ��ڱ�CD��BC���ӳ������ƶ�ʱ������AE��DF����1���еĽ��ۻ������𣿣�����ֱ�ӻش���������������������֤����������AC������ACEΪ����������ʱCE��CD��ֵ��
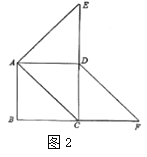
��3����ͼ3����E��F�ֱ���ֱ��DC��CB���ƶ�ʱ������AE��DF���ڵ�P�����ڵ�E��F���ƶ���ʹ�õ�PҲ��֮�˶������㻭����P�˶�·���IJ�ͼ.��AD=2��������߶�CP�����ֵ.

ͼ1 ͼ2 ͼ3
���𰸡���1��AE=DF��AE��DF�����ɼ���������2��������CE:CD=![]() ��2����3��
��2����3�� ![]()
�������������������1�����������ε����ʣ���SAS��֤����ADE�ա�DCF����ȫ�������ε����ʵ�AE=DF����DAE=��CDF�����ɵȽǵ������ȿɵ�AE��DF��
��2��������������ٵ�AC=CEʱ����������ABCD�ı߳�Ϊa���ɹ��ɶ������AC=CE=![]() a���ɣ��ڵ�AE=ACʱ���������εı߳�Ϊa���ɹ��ɶ������AC=AE=
a���ɣ��ڵ�AE=ACʱ���������εı߳�Ϊa���ɹ��ɶ������AC=AE=![]() a�����������ε�����֪��ADC=90�㣬Ȼ����ݵ��������ε����ʵó�DE=CD=a���ɣ�
a�����������ε�����֪��ADC=90�㣬Ȼ����ݵ��������ε����ʵó�DE=CD=a���ɣ�
��3���ɣ�1����2��֪����P��·����һ����ADΪֱ����Բ����AD���е�ΪQ������QC�����ڵ�P����ʱCP�ij���������ɹ��ɶ����ɵ�QC�ij�������CP���ɣ�
�����������1��AE=DF��AE��DF��
�����ǣ����ı���ABCD�������Σ�
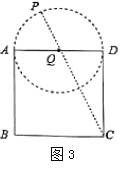
��AD=DC����ADE=��DCF=90����
�߶���E��F�ֱ��D��C����ͬʱ����������ͬ���ٶ���ֱ��DC��CB���ƶ���
��DE=CF��
����ADE����DCF��
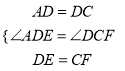 ��
��
��![]() ��
��
��AE=DF����DAE=��FDC��
�ߡ�ADE=90�������ADP+��CDF=90����
���ADP+��DAE=90����
���APD=180��-90��=90����
��AE��DF��
��2����1���еĽ��ۻ�������
�����������
����ͼ1����AC=CEʱ��
��������ABCD�ı߳�Ϊa���ɹ��ɶ����ã�
![]() ��
��
��![]() ��
��
����ͼ2����AE=ACʱ��
��������ABCD�ı߳�Ϊa���ɹ��ɶ����ã�
![]() ��
��
���ı���ABCD�������Σ�
���ADC=90������AD��CE��
��DE=CD=a��
��CE:CD=2a:a=2��
��CE:CD=![]() ��2��
��2��
��3���ߵ�P���˶��б��֡�APD=90����
���P��·������ADΪֱ����Բ��
��ͼ3����AD���е�ΪQ������CQ���ӳ���Բ���ڵ�P��
��ʱCP�ij������
����Rt��QDC�� ![]()
��![]() ��
��
���߶�CP�����ֵ��![]() .
.


 �߽�������ϵ�д�
�߽�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
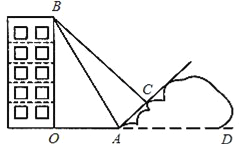
����Ŀ��ijУ���꼶��С��ͬѧ�����Լ��Ҹ������в���һ��¥���߶ȵ�ʵ�������ͼ������ɽ���½�A���������¥����¥��B�������Ϊ60�㣬��ɽ�������ߵ�C���ٲ��B�������Ϊ45�㣮��֪OA=200m����ɽ�µ��±�i=![]() ����O��A��D��ͬһ��ֱ���ϣ�
����O��A��D��ͬһ��ֱ���ϣ�
��1��¥��OB�ĸ߶ȣ�
��2��С����ɽ�����߹��ľ���AC����������̺ͽ������ȡ����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ���˽���и��꼶ѧ��ÿ���ƽ��˯��ʱ�䣨��λ��h����ȷ��1 h�������������˲���ѧ�������õõ������ݻ���������������������ͳ��ͼ��
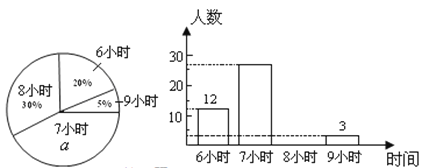
�������ͼ���ṩ����Ϣ���ش��������⣺
��1���������ͳ��ͼ�аٷ���![]() ��ֵΪ_______��������ѧ������Ϊ______��
��ֵΪ_______��������ѧ������Ϊ______��
��2�����ƽ��˯��ʱ��Ϊ8Сʱ������������ȫ����ͼ��
��3������ⲿ��ѧ����ƽ��˯��ʱ���ƽ������
��4�������У����ѧ��1200�����������˯�߲��㣨����8Сʱ����ѧ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������߳��ֱ�Ϊa��b��![]() >
>![]() ����������ֽƬ������һ�𣮣��ú���a��b�Ĵ���ʽ��ʾ����Ľ����
����������ֽƬ������һ�𣮣��ú���a��b�Ĵ���ʽ��ʾ����Ľ����
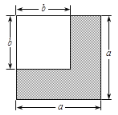
�������������ַ������ͼ����Ӱ���ֵ������
�� �������ȣ��㷢���������ĵ�����ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ڳ��������л�����Ĵ�ͳϰ�ߣ�ũ�����³����糿��С���������ò�������װ��һЩ���ӣ����ӳ�ʳ�IJ�ͬ�⣬����һ����ͬ��������Ŵ��������������һЩ�����գ���С�����������ó�һ����Ŵ���յĸ���Ϊ![]() ��
��
��1��������������յĸ�����
��2��С����һ�������ó�һ�����ӣ����Żأ����ڶ������ó�һ�����ӣ�����������ͼ���б�������С�������õ��Ķ��������յĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ɽ��������չ����ҵ���������ַ������������ڡ��γ�ǧ���顢�������ס���������������Щ���ʣ�����ͬѧ�Ƕ����������ˣ���˽����������������οͽӴ����������Ȳ�������2015��Ӵ�1800���˴Σ�2015����2017���������ۼƽӴ��οߴ�5958���˴�.
(1)����ɽ��2015����2017�����οͽӴ�������ƽ��������.
(2)�������ʸ�������������Ԥ��2018�����οͽӴ��������Ƶ����˴Σ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
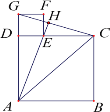
����Ŀ����ͼ����֪�ı���![]() ���ı���
���ı���![]() Ϊ�����Σ���
Ϊ�����Σ���![]() ���߶�
���߶�![]() �ϣ���
�ϣ���![]() ��ͬһֱ���ϣ�����
��ͬһֱ���ϣ�����![]() �����ӳ�
�����ӳ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
��1����֤��![]() ��
��
��2����![]() ��
��![]() �����߶�
�����߶�![]() �ij���
�ij���
��3����![]() ��
��![]() ������H���߶�GC���е�ʱ����
������H���߶�GC���е�ʱ����![]() ��
��![]() ����ʲô���Ĺ�ϵʽ.
����ʲô���Ĺ�ϵʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ������л�����ѧ���ݽ������У���λ��ί�ֱ���ס�����λѡ�ֵ��������£��ף�8��7��9��8��8���ң�7��9��6��9��9��������˵���д�����ǣ�������
A. �÷ֵķ�����ҵ÷ֵķ���СB. �÷ֵ�������8���ҵ÷ֵ�������9
C. �ס��ҵ÷ֵ�ƽ��������8D. �÷ֵ���λ����9���ҵ÷ֵ���λ����6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
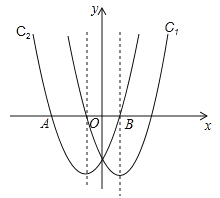
����Ŀ����ͬһֱ������ϵ�У�������y=ax2��2x��3��������y=x2+mx+n����y��Գƣ�C2��x�ύ��A��B���㣬���е�A�ڵ�B����࣮
��1����������C1��C2�ĺ�������ʽ��
��2����A��B��������ꣻ
��3����������C1���Ƿ����һ��P����������C2���Ƿ����һ��Q��ʹ����ABΪ�ߣ�����A��B��P��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ������ڣ����P��Q��������ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com