
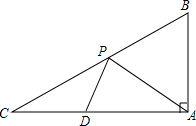
 如图,在△ABC中,∠BAC=90°,∠C=30°,AB=$\sqrt{3}$,点D在AC边上,且CD=$\frac{1}{2}$,点P是斜边BC上的一个动点,求PA+PD的最小值.
如图,在△ABC中,∠BAC=90°,∠C=30°,AB=$\sqrt{3}$,点D在AC边上,且CD=$\frac{1}{2}$,点P是斜边BC上的一个动点,求PA+PD的最小值. 分析 作点A关于BC的对称点E,AE交BC于F,则AE⊥BC,EF=AF,连接DE交BC于P,则PE=PA,从而确定PA+PD=PE+PD=DE的值最小,然后根据解直角三角形和勾股定理即可求得.
解答 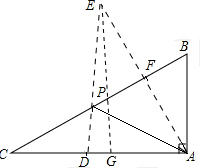 解:作点A关于BC的对称点E,AE交BC于F,则AE⊥BC,EF=AF,连接DE交BC于P,则PE=PA,
解:作点A关于BC的对称点E,AE交BC于F,则AE⊥BC,EF=AF,连接DE交BC于P,则PE=PA,
∴PA+PD=PE+PD=DE,
∴PA+PD的最小值为DE,
∵∠BAC=90°,∠C=30°,AB=$\sqrt{3}$,
∴∠B=60°,AC=$\frac{AB}{tan∠C}$=3,
在RT△ABF中,∠BAF=30°
∴AF=$\frac{\sqrt{3}}{2}$AB=$\frac{\sqrt{3}}{2}$×$\sqrt{3}$=$\frac{3}{2}$,
∴AE=2AF=3,
作EG⊥AC于G,则EG∥AB,
∴∠AEG=∠BAF=30°,
∴AG=$\frac{1}{2}$AE=$\frac{3}{2}$,EG=$\frac{\sqrt{3}}{2}$AE=$\frac{3}{2}$$\sqrt{3}$
∴DG=AC-CD-AG=3-$\frac{1}{2}$-$\frac{3}{2}$=1,
在RT△EGD中,ED=$\sqrt{E{G}^{2}+D{G}^{2}}$=$\frac{\sqrt{31}}{2}$.
∴PA+PD的最小值为$\frac{\sqrt{31}}{2}$.
点评 此题考查了轴对称-最短路线的问题,解直角三角函数,确定动点E何位置时,作出辅助线构建直角三角形是关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | a2>ab | B. | a+c>b+c | C. | $\frac{a}{c^2}>\frac{b}{c^2}$ | D. | c-a<c-b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
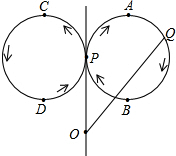 如右图所示,点Q表示蜜蜂,它从点P出发,按照着箭头所示的方向沿P→A→B→P→C→D→P的路径匀速飞行,此飞行路径是一个以直线l为对称轴的轴对称图形,在直线l上的点O处(点O与点P不重合)利用仪器测量了∠POQ的大小.设蜜蜂飞行时间为x,∠POQ的大小为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
如右图所示,点Q表示蜜蜂,它从点P出发,按照着箭头所示的方向沿P→A→B→P→C→D→P的路径匀速飞行,此飞行路径是一个以直线l为对称轴的轴对称图形,在直线l上的点O处(点O与点P不重合)利用仪器测量了∠POQ的大小.设蜜蜂飞行时间为x,∠POQ的大小为y,则下列图象中,能表示y与x的函数关系的图象大致是( )| A. | 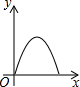 | B. | 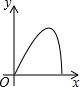 | C. | 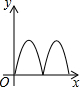 | D. | 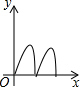 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
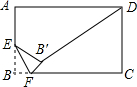 如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC边上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是2$\sqrt{10}$-2.
如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC边上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是2$\sqrt{10}$-2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
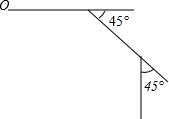 如图,小峰从点O出发,前进5m后向右转45°,再前进5m后又向右转45°,…,这样一直走下去,他第一次回到出发点O时,一共走的路程是40m.
如图,小峰从点O出发,前进5m后向右转45°,再前进5m后又向右转45°,…,这样一直走下去,他第一次回到出发点O时,一共走的路程是40m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | -6 | C. | $\frac{2}{15}$ | D. | -$\frac{2}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
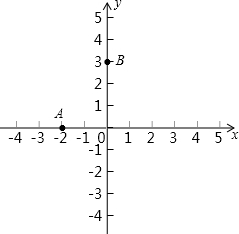 如图,平面直角坐标系中,点A在x轴上,点B在y轴上,OA=2,OB=3.
如图,平面直角坐标系中,点A在x轴上,点B在y轴上,OA=2,OB=3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com