
定义:底与腰的比是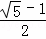 的等腰三角形叫做黄金等腰三角形.
的等腰三角形叫做黄金等腰三角形.
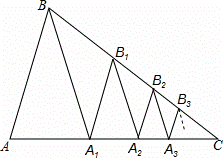
如图,已知△ABC中,AB=BC,∠C=36°,BA1平分∠ABC交AC于A1.
(1)证明:AB2=AA1•AC;
(2)探究:△ABC是否为黄金等腰三角形?请说明理由;(提示:此处不妨设AC=1)
(3)应用:已知AC=a,作A1B1∥AB交BC于B1,B1A2平分∠A1B1C交AC于A2,作A2B2∥AB交B2,B2A3平分∠A2B2C交AC于A3,作A3B3∥AB交BC于B3,…,依此规律操作下去,用含a,n的代数式表示An﹣1An.(n为大于1的整数,直接回答,不必说明理由)
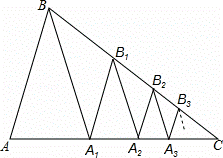
解答: (1)证明:∵AC=BC,∠C=36°,
∴∠A=∠ABC=72°,
∵BA1平分∠ABC,
∴∠ABA1=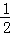 ∠ABC=36°,
∠ABC=36°,
∴∠C=∠ABA1,
又∵∠A=∠A,
∴△ABC∽△AA1B,
∴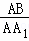 =
=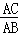 ,即AB2=AA1•AC;
,即AB2=AA1•AC;
(2)解:△ABC是黄金等腰三角形,
理由:由(1)知,AB2=AC•AA1,
设AC=1,
∴AB2=AA1,
又由(1)可得:AB=A1B,
∵∠A1BC=∠C=36°,
∴A1B=A1C,
∴AB=A1C,
∴AA1=AC﹣A1C=AC﹣AB=1﹣AB,
∴AB2=1﹣AB,
设AB=x,即x2=1﹣x,
∴x2+x﹣1=0,
解得:x1=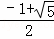 ,x2=
,x2=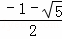 (不合题意舍去),
(不合题意舍去),
∴AB=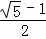 ,
,
又∵AC=1,
∴ =
=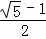 ,
,
∴△ABC是黄金等腰三角形;
(3)解:由(2)得;当AC=a,则AA1=AC﹣A1C=AC﹣AB=a﹣AB=a﹣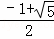 a=
a=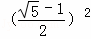 a,
a,
同理可得:A1A2=A1C﹣A1B1=AC﹣AA1﹣A1B1
=a﹣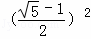 a﹣
a﹣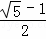 A1C
A1C
=a﹣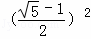 a﹣
a﹣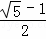 [a﹣
[a﹣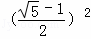 a]
a]
=(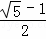 )3a.
)3a.
故An﹣1An= a.
a.


科目:初中数学 来源: 题型:
据报道,2015年全国普通高考报考人数约为9 420 000人,数据9 420 000用科学记数法表示为9.42×10n,则n的值是( )
A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知反比例函数y=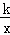 的图象经过点A(﹣3,﹣2).
的图象经过点A(﹣3,﹣2).
(1)求反比例函数的解析式;
(2)若点B(1,m),C(3,n)在该函数的图象上,试比较m与n的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
近年来,“在初中数学教学中使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了若干名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和统计图:
学生对使用计算器影响计算能力发展的看法统计表
看法 没有影响 影响不大 影响很大
学生人数 100 60 m
根据以上图表信息,解答下列问题:
(1)统计表中的m= ;
(2)统计图中表示“影响不大”的扇形的圆心角度数为 度;
(3)从这次接受调查的学生中随机调查一人,恰好是持“影响很大”看法的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
某几何体由一些大小相同的小正方体组成,如图分别是它的主视图和俯视图,那么要组成该几何体,至少需要多少个这样的小正方体( )

A.3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
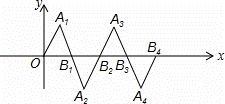
在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是( )
A. (4n﹣1,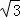 ) B. (2n﹣1,
) B. (2n﹣1,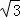 ) C. (4n+1,
) C. (4n+1,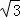 ) D. (2n+1,
) D. (2n+1,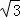 )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中.顶点为(﹣4,﹣1)的抛物线交y轴于点A(0,3),交x轴于B,C两点.
(1)求此抛物线的解析式;
(2)已知点P是抛物线上位于B,C两点之间的一个动点,问:当点P运动到什么位置时,四边形ABPC的面积最大?并求出此时四边形ABPC的面积.
(3)过点B作AB的垂线交抛物线于点D,是否存在以点C为圆心且与线段BD和抛物线的对称轴l同时相切的圆?若存在,求出圆的半径;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
(1)求证:DC=DE;
(2)若tan∠CAB=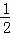 ,AB=3,求BD的长.
,AB=3,求BD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com