
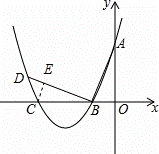
如图,在平面直角坐标系中.顶点为(﹣4,﹣1)的抛物线交y轴于点A(0,3),交x轴于B,C两点.
(1)求此抛物线的解析式;
(2)已知点P是抛物线上位于B,C两点之间的一个动点,问:当点P运动到什么位置时,四边形ABPC的面积最大?并求出此时四边形ABPC的面积.
(3)过点B作AB的垂线交抛物线于点D,是否存在以点C为圆心且与线段BD和抛物线的对称轴l同时相切的圆?若存在,求出圆的半径;若不存在,请说明理由.

解:(1)根据题意,可设抛物线的解析式为y=a(x+4)2﹣1,
把点A(0,3)代入得:3=16a﹣1,
解得a=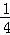 ,
,
所以此抛物线的解析式为y=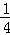 (x+4)2﹣1;
(x+4)2﹣1;
(2)令y=0,则0=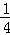 (x+4)2﹣1;
(x+4)2﹣1;
解得x1=﹣2,x2=﹣6,
∴B(﹣2,0),C(﹣6,0),
∴BC=4,
∵S四边形ABPC=S△ABC+S△PBC,S△ABC=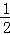 BC•OA=
BC•OA=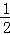 ×4×3=6,
×4×3=6,
∴要使四边形ABPC的面积最大,则△PBC的面积最大,
∴当P点移动到抛物线的顶点是△PBC的面积最大,
∴四边形ABPC的面积的最大值为:S△ABC+S△PBC=6+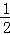 ×4×1=6+2=8;
×4×1=6+2=8;
(3)如图,设⊙C与BD相切于点E,连接CE,则∠BEC=∠AOB=90°.
∵A(0,3)、B(﹣2,0)、C(﹣6,0),
∴OA=3,OB=2,OC=6,BC=4;
∴AB=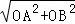 =
=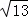 ,
,
∵AB⊥BD,
∴∠ABC=∠EBC+90°=∠OAB+90°,
∴∠EBC=∠OAB,
∴△OAB∽△EBC,
∴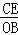 =
=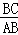 ,即
,即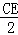 =
=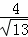
∴EC=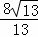 .
.
设抛物线对称轴交x轴于F.
∵抛物线的对称轴x=﹣4,
∴CF=2≠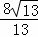 ,
,
∴不存在以点C为圆心且与线段BD和抛物线的对称轴l同时相切的圆.


科目:初中数学 来源: 题型:
在平面直角坐标系中,点A(﹣2,1)与点B关于原点对称,则点B的坐标为( )
A.(﹣2,1) B. (2,﹣1) C. (2,1) D. (﹣2,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
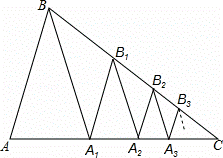
定义:底与腰的比是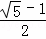 的等腰三角形叫做黄金等腰三角形.
的等腰三角形叫做黄金等腰三角形.
如图,已知△ABC中,AB=BC,∠C=36°,BA1平分∠ABC交AC于A1.
(1)证明:AB2=AA1•AC;
(2)探究:△ABC是否为黄金等腰三角形?请说明理由;(提示:此处不妨设AC=1)
(3)应用:已知AC=a,作A1B1∥AB交BC于B1,B1A2平分∠A1B1C交AC于A2,作A2B2∥AB交B2,B2A3平分∠A2B2C交AC于A3,作A3B3∥AB交BC于B3,…,依此规律操作下去,用含a,n的代数式表示An﹣1An.(n为大于1的整数,直接回答,不必说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
现在的青少年由于沉迷电视、手机、网络游戏等,视力日渐减退,某市为了解学生的视力变化情况,从全市九年级随机抽取了1500名学生,统计了每个人连续三年视力检查的结果,根据视力在4.9以下的人数变化制成折线统计图,并对视力下降的主要因素进行调查,制成扇形统计图.
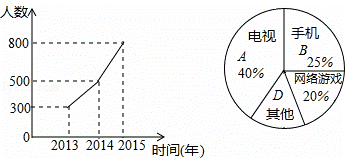
解答下列问题:
(1)图中D所在扇形的圆心角度数为 54° ;
(2)若2015年全市共有30000名九年级学生,请你估计视力在4.9以下的学生约有多少名?
(3)根据扇形统计图信息,你觉得中学生应该如何保护视力?
查看答案和解析>>
科目:初中数学 来源: 题型:
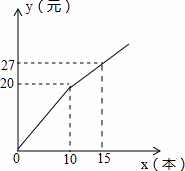
小明到超市买练习本,超市正在打折促销:购买10本以上,从第11 本开始按标价打折优惠,买练习本所花费的钱数y(元)与练习本的个数x(本)之间的关系如图所示,那么在这个超市买10本以上的练习本优惠折扣是 折.
本开始按标价打折优惠,买练习本所花费的钱数y(元)与练习本的个数x(本)之间的关系如图所示,那么在这个超市买10本以上的练习本优惠折扣是 折.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在直角坐标系xOy中,点A,B分别在x轴和y轴,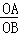 =
=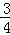 .∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=
.∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=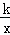 的图象过点C.当以CD为边的正方形的面积为
的图象过点C.当以CD为边的正方形的面积为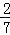 时,k的值是( )
时,k的值是( )
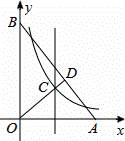
A. 2 B. 3 C. 5 D. 7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com