
【题目】已知AC⊥BC于C,BC=a,CA=b,AB=c,下列选项中⊙O的半径为![]() 的是( )
的是( )
A. 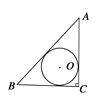 B.
B. 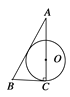 C.
C. 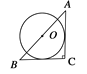 D.
D. 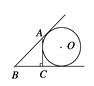
【答案】C
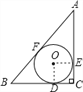
【解析】A. 设圆的半径是x,圆切AC于E,切BC于D,切AB于F,如图(1)同样得到正方形OECD,AE=AF,BD=BF,则ax+bx=c,求出x=![]() ,故本选项错误;
,故本选项错误;
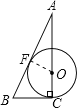
B. 设圆切AB于F,圆的半径是y,连接OF,如图(2),
则△BCA∽△OFA,∴![]() ,
,
∴![]() ,解得:y=
,解得:y=![]() ,故本选项错误;
,故本选项错误;
C. 连接OE、OD,
∵AC、BC分别切圆O于E. D,
∴∠OEC=∠ODC=∠C=90°,
∵OE=OD,
∴四边形OECD是正方形,
∴OE=EC=CD=OD,
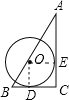
设圆O的半径是r,
∵OE∥BC,∴∠AOE=∠B,
∵∠AEO=∠ODB,
∴△ODB∽△AEO,
∴![]() ,
,![]() ,
,
解得:r=![]() ,故本选项正确;
,故本选项正确;
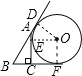
从上至下三个切点依次为D,E,F;并设圆的半径为x;
容易知道BD=BF,所以AD=BDBA=BFBA=a+xc;
又∵bx=AE=AD=a+xc;所以x=![]() ,故本选项错误。
,故本选项错误。
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,已知E、F分别是ABCD的边BC、AD上的点,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)若四边形AECF是菱形,且BC=10,∠BAC=90°,求BE的长.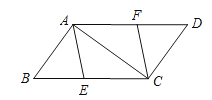
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明根据去年1~8月本班同学参加学校组织的“书香校园”活动中全班同学的课外阅读书籍的数量(单位:本),绘制了如图所示折线统计图,下列说法正确的是( )
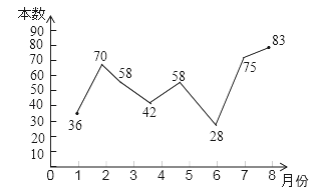
A. 阅读数量的平均数是57 B. 阅读数量的众数是42
C. 阅读数量的中位数是58 D. 有4个月的阅读数量超过60本
查看答案和解析>>
科目:初中数学 来源: 题型:
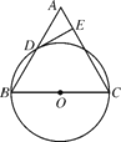
【题目】如图,已知在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)若⊙O的直径为18,cosB=![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com