
【题目】如图1,笔直的公路上有A、B两个站点相距40km,在公路的同侧有C、D两个村庄,DA⊥AB,CB⊥AB,且DA=20km,CB=10km,现政府决定在A、B之间建一个土特产加工基地E.
(1)若要使土特产加工基地E点到C、D两村的距离相等,请用直尺和圆规在图1中作出点E;
(2)在(1)的条件下求出基地E到A站的距离;
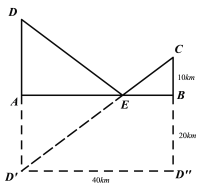
(3)若要使土特产加工基地E点到C、D两村的距离和(即DE +EC)最小,求出此最小的距离和.

【答案】(1)见解析;(2)![]() ;(3)50km
;(3)50km
【解析】
(1)连接CD作CD的垂直平分线交AB于点E;
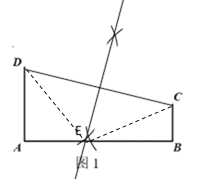
(2)连接DE、CE,利用线段的垂直平分线的性质得到DE=CE,再根据勾股定理建立等式求出AE;
(3)作点D关于AB的对称点![]() ,连接C,
,连接C,![]() 交AB于点E,(DE+CE)的最小值即为(
交AB于点E,(DE+CE)的最小值即为(![]() E+EC)的值,延长CB至点
E+EC)的值,延长CB至点![]() ,使B
,使B![]() =A
=A![]() =AD=20km,则四边形A
=AD=20km,则四边形A![]()
![]() B是矩形,
B是矩形,
利用勾股定理求出答案即可.
解:(1)如图
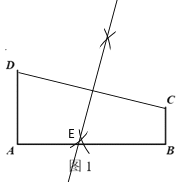
(2)连接DE、CE,
![]() ,
,
∴DE=CE,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴AE=![]() ;
;
(3)作点D关于AB的对称点![]() ,连接C,
,连接C,![]() 交AB于点E,(DE+CE)的最小值即为(
交AB于点E,(DE+CE)的最小值即为(![]() E+EC)的值,
E+EC)的值,
延长CB至点![]() ,使B
,使B![]() =A
=A![]() =AD=20km,则四边形A
=AD=20km,则四边形A![]()
![]() B是矩形,
B是矩形,
∴![]()
![]() =AB=40km,
=AB=40km,
∵BC=10km,
∴C![]() =30km,
=30km,
∴![]() E+EC= C
E+EC= C![]() =
=![]() =50km.
=50km.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=![]() 的图象相交于点A(m,3)、B(﹣6,n),与x轴交于点C.
的图象相交于点A(m,3)、B(﹣6,n),与x轴交于点C.
(1)求一次函数y=kx+b的关系式;
(2)结合图象,直接写出满足kx+b>![]()
![]() 的x的取值范围;
的x的取值范围;
(3)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标.
S△BOC,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
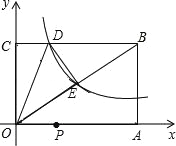
【题目】如图,已知矩形OABC的两边OA、OC分别落在x轴、y轴的正半轴上,顶点B的坐标是(6,4),反比例函数y=![]() (x>0)的图象经过矩形对角线的交点E,且与BC边交于点D.
(x>0)的图象经过矩形对角线的交点E,且与BC边交于点D.
(1)①求反比例函数的解析式与点D的坐标;②直接写出△ODE的面积;
(2)若P是OA上的动点,求使得“PD+PE之和最小”时的直线PE的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
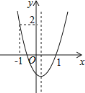
【题目】如图,二次函数![]() 的图象开口向上,图象经过点
的图象开口向上,图象经过点![]() 和
和![]() ,且与
,且与![]() 轴相交于负半轴.
轴相交于负半轴.
第![]() 问:给出四个结论:①
问:给出四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .写出其中正确结论的序号(答对得
.写出其中正确结论的序号(答对得![]() 分,少选、错选均不得分)
分,少选、错选均不得分)
第 ![]() 问:给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.写出其中正确结论的序号.
问:给出四个结论:①abc<0;②2a+b>0;③a+c=1;④a>1.写出其中正确结论的序号.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() ,
,
(1)通过配方,写出其对称轴,顶点坐标;
(2)分别求出其与![]() 轴、
轴、![]() 轴的交点坐标;
轴的交点坐标;
(3)画出函数的大致图象,结合图象说明,当![]() 取何值时,
取何值时,![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
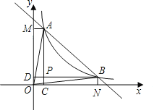
【题目】已知反比例函数![]() 的图象与直线
的图象与直线![]() 相交于第一象限
相交于第一象限![]() 、
、![]() 的两点.如图所示,过
的两点.如图所示,过![]() 、
、![]() 两点分别作
两点分别作![]() 、
、![]() 轴的垂线,线段
轴的垂线,线段![]() 、
、![]() 相交与
相交与![]() ,给出以下结论:①
,给出以下结论:①![]() ;②四边形
;②四边形![]() 是正方形;③若
是正方形;③若![]() .则
.则![]() 的面积是
的面积是![]() ;④
;④![]() 点一定在直线
点一定在直线![]() 上,其中正确命题的个数是几个( )
上,其中正确命题的个数是几个( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | |
摸到白球的次数m | 58 | 116 | 295 | 484 | 601 | |
摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.605 | 0.601 |
(1)计算并完成上述表格;
(2)请估计:当n很大时,摸到白球的频率将会接近;(精确到0.1)
(3)请你估算口袋中白球的数量接近多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
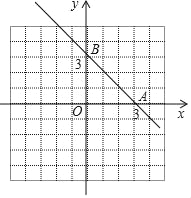
【题目】如图,抛物线y=﹣x2+bx+c经过直线y=﹣x+3与坐标轴的两个交点A、B,与x轴的另一个交点为C,顶点为D.
(1)求抛物线的解析式;
(2)画出抛物线的图象;
(3)在x轴上是否存在点N使△ADN为直角三角形?若存在,求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com