
【题目】已知反比例函数![]() 的图象与直线
的图象与直线![]() 相交于第一象限
相交于第一象限![]() 、
、![]() 的两点.如图所示,过
的两点.如图所示,过![]() 、
、![]() 两点分别作
两点分别作![]() 、
、![]() 轴的垂线,线段
轴的垂线,线段![]() 、
、![]() 相交与
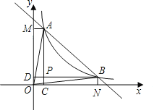
相交与![]() ,给出以下结论:①
,给出以下结论:①![]() ;②四边形
;②四边形![]() 是正方形;③若
是正方形;③若![]() .则
.则![]() 的面积是
的面积是![]() ;④
;④![]() 点一定在直线
点一定在直线![]() 上,其中正确命题的个数是几个( )
上,其中正确命题的个数是几个( )
A. 4 B. 3 C. 2 D. 1
【答案】A
【解析】
①先求出直线![]() 与两坐标轴的交点坐标可得出△OEF是等腰直角三角形,故E、F两点关于直线y=x对称,再由反比例函数的图象关于直线y=x对称可知A、B两点关于直线y=x对称,故可得出y=x是线段AB的垂直平分线,由此即可得出结论;
与两坐标轴的交点坐标可得出△OEF是等腰直角三角形,故E、F两点关于直线y=x对称,再由反比例函数的图象关于直线y=x对称可知A、B两点关于直线y=x对称,故可得出y=x是线段AB的垂直平分线,由此即可得出结论;
②根据AM⊥y轴,BD⊥y轴,AC⊥x轴,BN⊥x轴可得出四边形ACOM与四边形BDON均是长方形,根据OA=OB可知AC=BD,故OC=OD,由此可得出结论;
③设![]() ,则B
,则B![]() ,P(x,x),再由点A在直线y=-x+6上,求出x的值即可得出A点坐标,再由三角形的面积公式求解即可;
,P(x,x),再由点A在直线y=-x+6上,求出x的值即可得出A点坐标,再由三角形的面积公式求解即可;
④根据点A、B关于直线y=x对称可知,OM=ON,再由AM⊥y轴,AC⊥x轴,BD⊥y轴,BN⊥x轴可知,四边形AMOC与四边形BDON均是矩形,由②知AM=BN,故OC=OD,所以AP=PB,所以点P在线段AB的垂直平分线上,所以点P在直线y=x上.
①∵令x=0,则y=6,令y=0,则x=6,
∴E(0,6),F(6,0),
∴E、F两点关于直线y=x对称,
∵反比例函数的图象关于直线y=x对称,
∴A、B两点关于直线y=x对称,
∴y=x是线段AB的垂直平分线,
∴OA=OB,故①正确;
②∵AM⊥y轴,BD⊥y轴,AC⊥x轴,BN⊥x轴,
∴四边形ACOM与四边形BDON均是长方形。
∵OA=OB,A.B两点关于直线y=x对称,
∴AC=BD,
∴OC=OD,
∴四边形OCPD是正方形,故②正确;
③设![]() ,则B
,则B![]() ,,P(x,x),
,,P(x,x),
∵点A在直线y=x+6上,
∴![]() 解得
解得![]()
∴A(1,5),B(5,1),
∴BP=AP=51=4,
∴![]() 故③正确;
故③正确;
④∵点A.B关于直线y=x对称,
∴OM=ON,
∵AM⊥y轴,AC⊥x轴,BD⊥y轴,BN⊥x轴,
∴四边形AMOC与四边形BDON均是矩形,
∵由②知AM=BN,
∴OC=OD,
∴AP=PB,
∴点P在线段AB的垂直平分线上,
∴点P在直线y=x上,故④正确.
故选:A.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
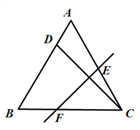
【题目】已知D是等边△ABC边AB上的一点,现将△ABC折叠,使点C与D重合,折痕为EF,点E、
F分别在AC和BC上.如图,若AD∶DB=1∶4,则CE∶CF=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
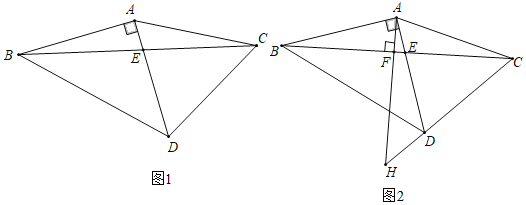
【题目】如图1,在△ABC中,AB=AC,以AB为直角边作等腰直角三角形ABD,与BC边交于点E,
(1)若∠ACE=18°,则∠ECD=
(2)探索:∠ACE与∠ACD有怎样的数量关系?猜想并证明.
(3)如图2,作△ABC的高AF并延长,交BD于点G,交CD延长线于点H,求证:CH2+DH2=2AD2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,笔直的公路上有A、B两个站点相距40km,在公路的同侧有C、D两个村庄,DA⊥AB,CB⊥AB,且DA=20km,CB=10km,现政府决定在A、B之间建一个土特产加工基地E.
(1)若要使土特产加工基地E点到C、D两村的距离相等,请用直尺和圆规在图1中作出点E;
(2)在(1)的条件下求出基地E到A站的距离;
(3)若要使土特产加工基地E点到C、D两村的距离和(即DE +EC)最小,求出此最小的距离和.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰三角形的一个外角为100°,则这个等腰三角形的顶角为________;等腰三角形一腰上的高与腰的夹角为36°,则该等腰三角形的顶角为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD中,E,F是对角线BD上的两点, 如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )

A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
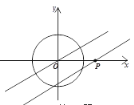
【题目】如图,直线![]() 的解析式为
的解析式为![]() ,⊙O是以坐标原点为圆心,半径为1的圆,点P在
,⊙O是以坐标原点为圆心,半径为1的圆,点P在![]() 轴上运动,过点P且与直线l平行(或重合)的直线与⊙O有公共点,则点P的横坐标为整数的点的个数有 _________个.
轴上运动,过点P且与直线l平行(或重合)的直线与⊙O有公共点,则点P的横坐标为整数的点的个数有 _________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 月初,西雅中学初二年级前往距离学校
月初,西雅中学初二年级前往距离学校![]() 的莲花镇基地研学.学生乘坐大巴,刘老师自行驾车前往,已知刘老师自行驾车的速度是大巴速度的
的莲花镇基地研学.学生乘坐大巴,刘老师自行驾车前往,已知刘老师自行驾车的速度是大巴速度的![]() 倍,他们同时从学校出发,结果刘老师比学生早
倍,他们同时从学校出发,结果刘老师比学生早![]() 到达目的地,
到达目的地,
(1)求大巴的速度;
(2)如果刘老师到基地后不停留,直接驾车到离基地![]() 的药店购买常用药以备不时之需,再赶回基地,其中在药店买药用时
的药店购买常用药以备不时之需,再赶回基地,其中在药店买药用时![]() 分钟.请问刘老师能在大巴到达之前赶回基地吗?
分钟.请问刘老师能在大巴到达之前赶回基地吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com