
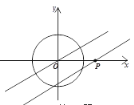
【题目】如图,直线![]() 的解析式为
的解析式为![]() ,⊙O是以坐标原点为圆心,半径为1的圆,点P在
,⊙O是以坐标原点为圆心,半径为1的圆,点P在![]() 轴上运动,过点P且与直线l平行(或重合)的直线与⊙O有公共点,则点P的横坐标为整数的点的个数有 _________个.
轴上运动,过点P且与直线l平行(或重合)的直线与⊙O有公共点,则点P的横坐标为整数的点的个数有 _________个.
【答案】5
【解析】
∵直线l的解析式为y=![]() x,
x,
∴∠1=30°,
当过点P且与直线l平行的直线与圆O相切,且切点在第二象限时,如图所示,
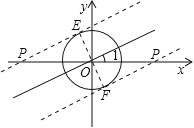
此时直线PE与圆O相切,切点为点E,
∵直线l∥PE,∠1=30°,
∴∠EPO=30°,
在Rt△PEO中,OE=1,
可得OP=2OE=2,又P在x轴负半轴上,
∴此时P坐标为(-2,0);
当过点P且与直线l平行的直线与圆O相切,且切点在第四象限时,如图所示,
此时直线PF与圆O相切,切点为点F,
∵直线l∥PF,∠1=30°,
∴∠FPO=30°,
在Rt△PFO中,OF=1,
可得OP=2OF=2,又P在x轴正半轴上,
∴此时P的坐标为(2,0),
综上,满足题意的点P横坐标p的范围是-2≤p≤2,
则点P的横坐标为整数的点的个数有-2,-1,0,1,2,共5个.


科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是⊙O的直径,AB=10,![]() ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=
,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=![]() ∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
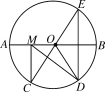
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图象与直线
的图象与直线![]() 相交于第一象限
相交于第一象限![]() 、
、![]() 的两点.如图所示,过
的两点.如图所示,过![]() 、
、![]() 两点分别作
两点分别作![]() 、
、![]() 轴的垂线,线段
轴的垂线,线段![]() 、
、![]() 相交与
相交与![]() ,给出以下结论:①
,给出以下结论:①![]() ;②四边形
;②四边形![]() 是正方形;③若
是正方形;③若![]() .则
.则![]() 的面积是
的面积是![]() ;④
;④![]() 点一定在直线
点一定在直线![]() 上,其中正确命题的个数是几个( )
上,其中正确命题的个数是几个( )
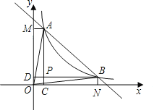
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
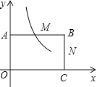
【题目】如图,在直角坐标系中,矩形![]() 的顶点
的顶点![]() 与坐标原点重合,顶点
与坐标原点重合,顶点![]() 、
、![]() 分别在坐标轴上,顶点
分别在坐标轴上,顶点![]() 的坐标为
的坐标为![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.
的中点.
(1)若反比例函数![]() 的图象经过点
的图象经过点![]() ,求该反比例函数的解析式,并通过计算判断点
,求该反比例函数的解析式,并通过计算判断点![]() 是否在该函数的图象上;
是否在该函数的图象上;
(2)若反比例函数![]() 的图象与
的图象与![]() (包括边界)有公共点,请直接写出
(包括边界)有公共点,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | |
摸到白球的次数m | 58 | 116 | 295 | 484 | 601 | |
摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.605 | 0.601 |
(1)计算并完成上述表格;
(2)请估计:当n很大时,摸到白球的频率将会接近;(精确到0.1)
(3)请你估算口袋中白球的数量接近多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
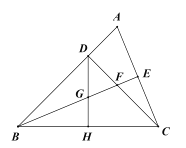
【题目】如图,![]() 中,
中,![]() ,
,![]() 于
于![]() ,
,![]() 平分
平分![]() ,
,![]() 于
于![]() ,与
,与![]() 相交于点
相交于点![]() ,
,![]() 是
是![]() 边的中点,连接
边的中点,连接![]() 与
与![]() 相交于点
相交于点![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() 是等腰三角形;④
是等腰三角形;④![]() .正确的有( )个.
.正确的有( )个.
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某广告公司设计一幅周长为16米的矩形广告牌,广告设计费为每平方米2000元.设矩形一边长为x,面积为S平方米.
(1)求S与x之间的函数关系式,并写出自变量x的取值范围;
(2)设计费能达到24000元吗?为什么?
(3)当x是多少米时,设计费最多?最多是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=ax2-2ax-1(a是常数,a≠0),下列结论正确的是( )
A. 当a=1时,函数图象过点(-1,1)
B. 当a=-2时,函数图象与x轴没有交点
C. 若a>0,则当x≥1时,y随x的增大而减小
D. 若a<0,则当x≤1时,y随x的增大而增大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com