
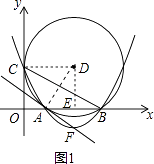
【题目】如图,在平面直角坐标系中,⊙D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6. 
(1)求圆的半径和点D的坐标;
(2)点A的坐标是 , 点B的坐标是 , sin∠ACB;
(3)求经过C、A、B三点的抛物线解析式;
(4)设抛物线的顶点为F,证明直线FA与⊙D相切.
【答案】
(1)解:过点D作DE⊥AB于E,连接DC、AD,如图1,
则AE=EB= ![]() AB=3,DC⊥y轴,
AB=3,DC⊥y轴,
∴∠DCO=∠COE=∠DEO=90°,
∴四边形OCDE是矩形,
∴OE=CD,DE=OC=4.
在Rt△ADE中,AD= ![]() =
= ![]() =5,
=5,
∴OE=CD=AD=5,
∴圆的半径为5,点D的坐标为(5,4);
(2)(2,0);(8,0);![]()
(3)解:设抛物线的解析式为y=ax2+bx+c,
∵A(2,0),B(8,0),C(0,4)在抛物线y=ax2+bx+c上,
∴  ,
,
解得 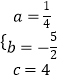 .
.
∴抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() x+4;
x+4;
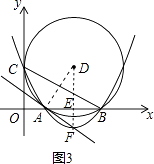
(4)解:连接DA,DF,如图3,
∵D、F都在线段AB的垂直平分线上,
∴DF垂直平分AB.
由y= ![]() x2﹣
x2﹣ ![]() x+4=
x+4= ![]() (x﹣5)2﹣
(x﹣5)2﹣ ![]() 可得F(5,﹣
可得F(5,﹣ ![]() ),
),
∵DF=4+ ![]() =
= ![]() ,AF=
,AF= ![]() =
= ![]() ,
,
∴DA2+AF2=52+( ![]() )2=
)2= ![]() =(
=( ![]() )2=DF2,
)2=DF2,
∴∠DAF=90°,
∴FA与⊙D相切.
【解析】解:(2)过点D作DE⊥AB于E,连接DB、AD,如图2, 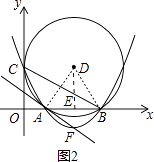
∵OE=5,AE=EB=3,
∴OA=5﹣3=2,OB=5+3=8.
∵DA=DB,
∴∠ADE=∠BDE= ![]() ∠ADB=∠ACB,
∠ADB=∠ACB,
∴sin∠ACB=sin∠ADE= ![]() =
= ![]() .
.
故答案分别为:(2,0),(8,0), ![]() ;
;
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠A=70°,∠B=90°,点A关于BC的对称点是A',点B关于AC的对称点是B',点C关于AB的对称点是C',若△ABC的面积是![]() ,则△A'B'C'的面积是_________________________.
,则△A'B'C'的面积是_________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
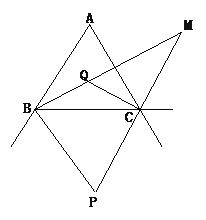
【题目】如图,△ABC的两外角平分线交于点P,易证∠P=90°-![]() ∠A;△ABC的两内角的平分线交于点Q,易证∠BQC=90°+
∠A;△ABC的两内角的平分线交于点Q,易证∠BQC=90°+![]() ∠A;那么△ABC的内角平分线BM与外角平分CM的夹角∠M=_____∠A.
∠A;那么△ABC的内角平分线BM与外角平分CM的夹角∠M=_____∠A.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A=150°.第一步:在△ABC上方确定一点A1,使∠A1BA=∠ABC,∠A1CA=∠ACB,如图1.第二步:在△A1BC上方确定一点A2,使∠A2BA1=∠A1BA,∠A2CA1=∠A1CA,如图2.照此下去,至多能进行( )步.
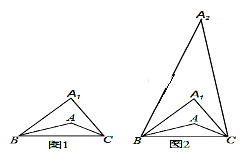
A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=3,连接DE,动点P从点B出发,以每秒1个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为__________秒时.△ABP和△DCE全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,求证:AD=DC+AB,
(2)如图②,在四边形ABCD中,AB∥DC,F是DC延长线上一点,连接AF,E是BC的中点,若AE是∠BAF的平分线,求证:AB=AF+CF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC. 
(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1=∠2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y= ![]() 的图象如图,以下结论:
的图象如图,以下结论:
①m<0;
②在每个分支上y随x的增大而增大;
③若点A(﹣1,a)、点B(2,b)在图象上,则a<b;
④若点P(x,y)在图象上,则点P1(﹣x,﹣y)也在图象上.
其中正确的个数是( )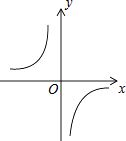
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在正方形ABCD的边CD上,把△ADE绕点A顺时针旋转90°至△ABF位置,如果AB= ![]() ,∠EAD=30°,那么点E与点F之间的距离等于 .
,∠EAD=30°,那么点E与点F之间的距离等于 . 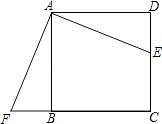
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com