
【题目】△ABC内接于⊙O,∠BAC的平分线交⊙O于D,交BC于E(BE>EC),过点D作⊙O的切线DF,交AB的延长线于F.
(1)求证:DF∥BC;
(2)连接OF,若tan∠BAC=![]() ,BD=
,BD=![]() ,DF=8,求OF的长.
,DF=8,求OF的长.
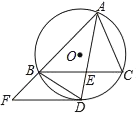
【答案】(1)证明见解析;(2)10.
【解析】
(1)根据切线的性质得:OD⊥DF,由角平分线得∠BAD=∠CAD,则所对的弧相等,由垂径定理得:OD⊥BC,从而得结论;
(2)先得∠BOD=∠BAC,根据tan∠BOD=![]() ,设ON=x,BN=
,设ON=x,BN=![]() ,利用勾股定理解决问题.
,利用勾股定理解决问题.
(1)证明:连接OD,
∵DF是⊙O的切线,
∴OD⊥DF,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴![]() ,
,
∴OD⊥BC,
∴DF∥BC;
(2)解:连接OB,
∵![]() ,
,
∴∠BOD=∠BAC,
由(1)知OD⊥BC,
∴tan∠BOD=![]() ,
,
∵tan∠BAC=2![]() ,
,
∴![]() ,
,
设ON=x,BN=2![]() x,
x,
由勾股定理得:OB=3x,
∴OD=3x,
∴DN=3x﹣x=2x,
Rt△BDN中,BN2+DN2=BD2,
∴![]() ,
,
解得x=2或﹣2(舍),
∴OB=OD=3x=6,
Rt△OFD中,由勾股定理得:OF=![]() =
=![]() =10.
=10.



科目:初中数学 来源: 题型:
【题目】(2011山东济南,27,9分)如图,矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线![]() 经过A、C两点,与AB边交于点D.
经过A、C两点,与AB边交于点D.
(1)求抛物线的函数表达式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式,并求出m为何值时,S取得最大值;
②当S最大时,在抛物线![]() 的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一笔直的海岸线上有A,B两个观测站,A在B的正东方向,有一艘小船停在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向,BP=6![]() km.
km.
(1)求A、B两观测站之间的距离;
(2)小船从点P处沿射线AP的方向前行,求观测站B与小船的最短距离.
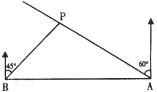
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线l:y=x+1交y轴于点A1,点A2,A3,…,An在直线l上,点B1,B2,B3,…,Bn在x轴的正半轴上,若△OA1B1,△A2B1B2,△A3B2B3,…,△AnBn﹣1Bn依次均为等腰直角三角形,则点B1的坐标是_____;点Bn的坐标是_____.
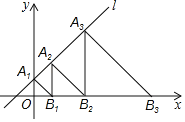
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠A=90°,CD平分∠ACB交AB于点D,O是BC上一点,经过C、D两点的⊙O分别交AC、BC于点E、F,AD=![]() ,∠ADC=60°,则劣弧
,∠ADC=60°,则劣弧![]() 的长为_____.
的长为_____.
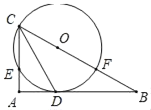
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD 中,对角线 AC 与 BD 相交于点 O ,点 E , F 分别为 OB , OD 的中点,延长 AE 至 G ,使 EG =AE ,连接 CG .
(1)求证: △ABE≌△CDF ;
(2)当 AB 与 AC 满足什么数量关系时,四边形 EGCF 是矩形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华优秀传统文化,某校开展“经典诵读”比赛活动,诵读材料有《论语》、《大学》、《中庸》(依次用字母A,B,C表示这三个材料),将A,B,C分别写在3张完全相同的不透明卡片的正面上,背面朝上洗匀后放在桌面上,比赛时小礼先从中随机抽取一张卡片,记下内容后放回,洗匀后,再由小智从中随机抽取一张卡片,他俩按各自抽取的内容进行诵读比赛.
(1)小礼诵读《论语》的概率是 ;(直接写出答案)
(2)请用列表或画树状图的方法求他俩诵读两个不同材料的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
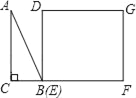
【题目】如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2![]() cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
A. 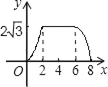 B.
B. 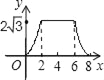 C.
C. 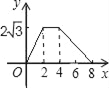 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌牛奶供应商提供A,B,C,D四种不同口味的牛奶供学生饮用.某校为了了解学生对不同口味的牛奶的喜好,对全校订牛奶的学生进行了随机调查,并根据调查结果绘制了如下两幅不完整的统计图.根据统计图的信息解决下列问题:

(1)本次调查的学生有多少人?
(2)补全上面的条形统计图;
(3)扇形统计图中C对应的中心角度数是_____;
(4)若该校有600名学生订了该品牌的牛奶,每名学生每天只订一盒牛奶,要使学生能喝到自己喜欢的牛奶,则该牛奶供应商送往该校的牛奶中,A,B口味的牛奶共约多少盒?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com