
【题目】如图,AB是⊙O的直径,AB=4 ![]() ,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.
,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB. 
(1)求证:CB是∠ECP的平分线;
(2)求证:CF=CE;
(3)当 ![]() =
= ![]() 时,求劣弧
时,求劣弧 ![]() 的长度(结果保留π)
的长度(结果保留π)
【答案】
(1)证明:∵OC=OB,
∴∠OCB=∠OBC,
∵PF是⊙O的切线,CE⊥AB,
∴∠OCP=∠CEB=90°,
∴∠PCB+∠OCB=90°,∠BCE+∠OBC=90°,
∴∠BCE=∠BCP,
∴BC平分∠PCE
(2)证明:连接AC.
∵AB是直径,
∴∠ACB=90°,
∴∠BCP+∠ACF=90°,∠ACE+∠BCE=90°,
∵∠BCP=∠BCE,
∴∠ACF=∠ACE,
∵∠F=∠AEC=90°,AC=AC,
∴△ACF≌△ACE,
∴CF=CE.
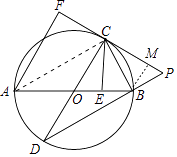
(3)解:作BM⊥PF于M.则CE=CM=CF,设CE=CM=CF=4a,PC=4a,PM=a,
∵△BMC∽△PMB,
∴ ![]() =
= ![]() ,
,
∴BM2=CMPM=3a2,
∴BM= ![]() a,
a,
∴tan∠BCM= ![]() =
= ![]() ,
,
∴∠BCM=30°,
∴∠OCB=∠OBC=∠BOC=60°,
∴ ![]() 的长=
的长= ![]() =
= ![]() π
π
【解析】(1)根据等角的余角相等证明即可;(2)欲证明CF=CE,只要证明△ACF≌△ACE即可;(3)作BM⊥PF于M.则CE=CM=CF,设CE=CM=CF=4a,PC=4a,PM=a,利用相似三角形的性质求出BM,求出tan∠BCM的值即可解决问题;
【考点精析】本题主要考查了垂径定理和切线的性质定理的相关知识点,需要掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】综合题
(1)【探索发现】如图①,是一张直角三角形纸片,∠B=60°,小明想从中剪出一个以∠B为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为 .
(2)【拓展应用】如图②,在△ABC中,BC=a,BC边上的高AD=h,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,则矩形PQMN面积的最大值为 . (用含a,h的代数式表示)
(3)【灵活应用】如图③,有一块“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角),求该矩形的面积.
(4)【实际应用】如图④,现有一块四边形的木板余料ABCD,经测量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC= ![]() ,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,AB=5,BC=3,先按图(2)操作:将矩形纸片ABCD沿过点A的直线折叠,使点D落在边AB上的点E处,折痕为AF;再按图(3)操作,沿过点F的直线折叠,使点C落在EF上的点H处,折痕为FG,则A、H两点间的距离为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
频数频率分布表
成绩x(分) | 频数(人) | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
根据所给信息,解答下列问题:
(1)m= , n=;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC=4cm,∠B=30°,点P从点B出发,以 ![]() cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发,以1cm/s的速度沿BA﹣AC方向运动到点C停止,若△BPQ的面积为y(cm2),运动时间为x(s),则下列最能反映y与x之间函数关系的图象是( )
cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发,以1cm/s的速度沿BA﹣AC方向运动到点C停止,若△BPQ的面积为y(cm2),运动时间为x(s),则下列最能反映y与x之间函数关系的图象是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,则下列6个代数式:ab、ac、a+b+c、2a+b、2a﹣b中,其值为正的式子的个数是( ) 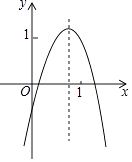
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF= ![]() BC,连接CD和EF.
BC,连接CD和EF. 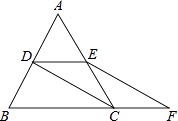
(1)求证:DE=CF;
(2)求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com