
【题目】如图,在等腰△ABC中,AB=AC=4cm,∠B=30°,点P从点B出发,以 ![]() cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发,以1cm/s的速度沿BA﹣AC方向运动到点C停止,若△BPQ的面积为y(cm2),运动时间为x(s),则下列最能反映y与x之间函数关系的图象是( )
cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发,以1cm/s的速度沿BA﹣AC方向运动到点C停止,若△BPQ的面积为y(cm2),运动时间为x(s),则下列最能反映y与x之间函数关系的图象是( )
A.
B.
C.
D.
【答案】D
【解析】解:作AH⊥BC于H,
∵AB=AC=4cm,
∴BH=CH,
∵∠B=30°,
∴AH= ![]() AB=2,BH=
AB=2,BH= ![]() AH=2
AH=2 ![]() ,
,
∴BC=2BH=4 ![]() ,
,
∵点P运动的速度为 ![]() cm/s,Q点运动的速度为1cm/s,
cm/s,Q点运动的速度为1cm/s,
∴点P从B点运动到C需4s,Q点运动到C需8s,
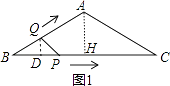
当0≤x≤4时,作QD⊥BC于D,如图1,BQ=x,BP= ![]() x,
x,
在Rt△BDQ中,DQ= ![]() BQ=
BQ= ![]() x,
x,
∴y= ![]()
![]() x
x ![]() x=
x= ![]() x2 ,
x2 ,
当4<x≤8时,作QD⊥BC于D,如图2,CQ=8﹣x,BP=4 ![]()
在Rt△BDQ中,DQ= ![]() CQ=
CQ= ![]() (8﹣x),
(8﹣x),
∴y= ![]()
![]() (8﹣x)4
(8﹣x)4 ![]() =﹣
=﹣ ![]() x+8
x+8 ![]() ,
,
综上所述,y= 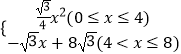 .
.
故选D.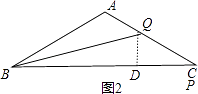
【考点精析】利用函数的图象对题目进行判断即可得到答案,需要熟知函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+b2 , 其中正确结论是(填序号)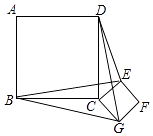
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AB=4 ![]() ,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.
,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB. 
(1)求证:CB是∠ECP的平分线;
(2)求证:CF=CE;
(3)当 ![]() =
= ![]() 时,求劣弧
时,求劣弧 ![]() 的长度(结果保留π)
的长度(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F. 
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘轮船位于灯塔P南偏西60°方向的A处,它向东航行20海里到达灯塔P南偏西45°方向上的B处,若轮船继续沿正东方向航行,求轮船航行途中与灯塔P的最短距离.(结果保留根号)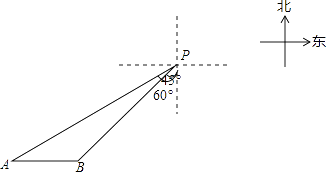
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,则下列6个代数式:ab、ac、a+b+c、2a+b、2a﹣b中,其值为正的式子的个数是( ) 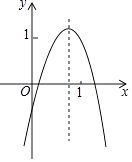
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有四个分别标有数字﹣1,﹣2,﹣3,﹣4的小球,它们的形状、大小、质地等完全相同.小强先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.
(1)用列表法或画树状图表示出(x,y)的所有可能出现的结果;
(2)求小强、小华各取一次小球所确定的点(x,y)落在一次函数y=x﹣1图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,我们把对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由.
(2)性质探究:试探索垂美四边形ABCD两组对边AB,CD与BC,AD之间的数量关系.
猜想结论:(要求用文字语言叙述)
写出证明过程(先画出图形,写出已知、求证).
(3)问题解决:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5,求GE长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com