
【题目】如图,△ABC中∠C=90°,线段AD是△ABC的角平分线,直线DE是线段AB的垂直平分线.若DE=1cm,DB=2cm,AC= ![]() cm.求点C到直线AD的距离.
cm.求点C到直线AD的距离. 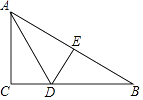
【答案】解:∵直线DE是线段AB的垂直平分线, ∴DA=DB=2cm,DE⊥AB,
∵线段AD是△ABC的角平分线,
∴DC=DE=1cm,
作CF⊥AD于F,则 ![]() ACCD=
ACCD= ![]() ADCF,
ADCF,
∴CF= ![]() =
= ![]() =
= ![]() ,
,
即点C到直线AD的距离为 ![]() .
.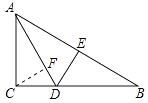
【解析】根据线段垂直平分线的性质得到DB=DC,根据角平分线的性质得到DE=AD,再根据直角三角形的面积计算得到答案即可.
【考点精析】解答此题的关键在于理解角平分线的性质定理的相关知识,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上,以及对线段垂直平分线的性质的理解,了解垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等.


科目:初中数学 来源: 题型:
【题目】某人购进一批苹果,到市场零售,已知销售额y(元)与卖出的苹果数量x(千克)的关系如表所示:则y与x之间的关系式为__________
数量x(千克) | 2 | 3 | 4 | 5 | … |
销售额y(元) | 7.2 | 10.8 | 14.4 | 18.0 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解我市2017年中考数学学科各分数段成绩分布情况,从中抽取180名考生的中考数学成绩进行统计分析.在这个问题中,样本是指( )
A. 180 B. 被抽取的180名考生
C. 被抽取的180名考生的中考数学成绩 D. 我市2017年中考数学成绩
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠A=∠ABC=90°,AD=10cm,BC=30cm,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
(1)求证:四边形BDFC是平行四边形;
(2)若△BCD是等腰三角形,求四边形BDFC的面积.
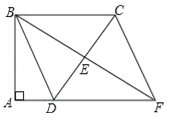
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,延长AB至E,延长CD至F,BE=DF,连接EF,与BC、AD分别相交于P、Q两点.
(1)求证:CP=AQ;
(2)若BP=1,PQ=![]() ,∠AEF=45°,求矩形ABCD的面积.
,∠AEF=45°,求矩形ABCD的面积.
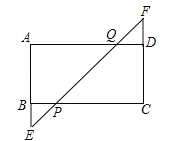
查看答案和解析>>
科目:初中数学 来源: 题型:
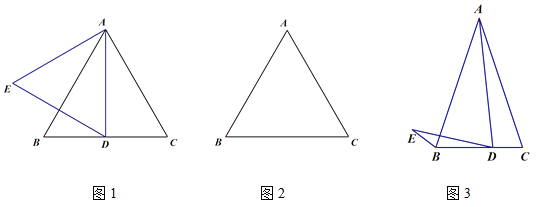
【题目】在等腰△ABC中,
(1)如图1,若△ABC为等边三角形,D为线段BC中点,线段AD关于直线AB的对称线段为线段AE,连接DE,则∠BDE的度数为___________;
(2)若△ABC为等边三角形,点D为线段BC上一动点(不与B,C重合),连接AD并将线段AD绕点D逆时针旋转60°得到线段DE,连接BE.
①根据题意在图2中补全图形;
②小玉通过观察、验证,提出猜测:在点D运动的过程中,恒有CD=BE.经过与同学们的充分讨论,形成了几种证明的思路:
思路1:要证明CD=BE,只需要连接AE,并证明△ADC≌△AEB;
思路2:要证明CD=BE,只需要过点D作DF∥AB,交AC于F,证明△ADF≌△DEB;
思路3:要证明CD=BE,只需要延长CB至点G,使得BG=CD,证明△ADC≌△DEG;
……
请参考以上思路,帮助小玉证明CD=BE.(只需要用一种方法证明即可)
(3)小玉的发现启发了小明:如图3,若AB=AC=kBC,AD=kDE,且∠ADE=∠C,此时小明发现BE,BD,AC三者之间满足一定的的数量关系,这个数量关系是______________________.(直接给出结论无须证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数,下面给出了求∠AGD的度数的过程,将此补充完整并在括号里填写依据. 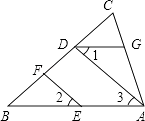
【解】∵EF∥AD(已知)
∴∠2=()
又∵∠1=∠2(已知)
∴∠1=∠3(等式性质或等量代换)
∴AB∥()
∴∠BAC+=180°()
又∵∠BAC=70°(已知)
∴∠AGD=110°(等式性质)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E是AD上的一点,且AE=![]() AD,对角线AC,BD交于点O,EC交BD于F,BE交AC于G,如果平行四边形ABCD的面积为S,那么,△GEF的面积为( )
AD,对角线AC,BD交于点O,EC交BD于F,BE交AC于G,如果平行四边形ABCD的面积为S,那么,△GEF的面积为( )
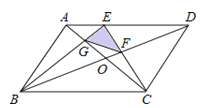
A. ![]() S B.
S B. ![]() S C.
S C. ![]() S D.
S D. ![]() S
S
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com