
【题目】![]() 个有理数两两的乘积是如下
个有理数两两的乘积是如下![]() 个数:
个数:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .请确定这
.请确定这![]() 个数并简述理由.
个数并简述理由.
【答案】-30,0.4,0.42,0.5,200或-200,-0.5,-0.42,-0.4,30.
【解析】
首先将将5个有理数两两的乘积由小到大排列,由5个有理数的两两乘积中有4个负数且没有0,可得这5个有理数中有1个负数和4个正数,或者1个正数和4个负数.再分别从若这5个有理数是1负4正,不妨设为x1<0<x2<x3<x4<x5,可得x1x5<x1x4<x1x3<x1x2<0<x2x3<x2x4<![]() <x3x5<x4x5,(其中x2x5和x3x4的大小关系暂时还不能断定),若这5个有理数是4负1正.不妨设为:x1<x2<x3<x4<0<x5,则x1x5<x2x5<x3x5<x4x5<0<x3x4<x2x4<
<x3x5<x4x5,(其中x2x5和x3x4的大小关系暂时还不能断定),若这5个有理数是4负1正.不妨设为:x1<x2<x3<x4<0<x5,则x1x5<x2x5<x3x5<x4x5<0<x3x4<x2x4<![]() <x1x3<x1x2,(其中x1x4和x2x3的大小关系暂时还不能断定),去分析求解即可求得答案.
<x1x3<x1x2,(其中x1x4和x2x3的大小关系暂时还不能断定),去分析求解即可求得答案.
将5个有理数两两的乘积由小到大排列:
-6000<-15<-12.6<-12<0.168<0.2<0.21<80<84<100.
∵5个有理数的两两乘积中有4个负数且没有0,
∴这5个有理数中有1个负数和4个正数,或者1个正数和4个负数.
(1)若这5个有理数是1负4正,不妨设为x1<0<x2<x3<x4<x5,
则x1x5<x1x4<x1x3<x1x2<0<x2x3<x2x4<![]() <x3x5<x4x5,(其中x2x5和x3x4的大小关系暂时还不能断定),
<x3x5<x4x5,(其中x2x5和x3x4的大小关系暂时还不能断定),
∴x1x5=-6000,x1x4=-15,x4x5=100,
三式相乘,得(x1x4x5)2=9×106,
又∵x1<0,x4>0,x5>0,
∴x1x4x5=-3000,
则x1=-30,x4=0.5,x5=200.
再由x1=-30,x1x2=-12,x1x3=-12.6,
得x2=0.4,x3=0.42.
经检验x1=-30,x2=0.4,x3=0.42,x4=0.5,x5=200满足题意.
(2)若这5个有理数是4负1正.不妨设为:x1<x2<x3<x4<0<x5,
则x1x5<x2x5<x3x5<x4x5<0<x3x4<x2x4<![]() <x1x3<x1x2,(其中x1x4和x2x3的大小关系暂时还不能断定),
<x1x3<x1x2,(其中x1x4和x2x3的大小关系暂时还不能断定),
∴x1x5=-6000,x2x5=-15,x1x2=100,
三式相乘,得(x1x2x5)2=9×106,
又∵x1<0,x2<0,x5>0,
解得x1x2x5=3000,
∴x1=-200,x2=-0.5,x5=30,
再由x5=30,x3x5=-12.6,x4x5=-12,
得x3=-0.42,x4=-0.4.
经检验,x1=-200,x2=-0.5,x3=-0.42,x4=-0.4,x5=30满足题意.
综上可得:这5个有理数分别是-30,0.4,0.42,0.5,200或-200,-0.5,-0.42,-0.4,30.


科目:初中数学 来源: 题型:
【题目】某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到江阴儿童福利院看望孤儿.如果分给每位儿童5盒牛奶,那么剩下18盒牛奶;如果分给每位儿童6盒牛奶,那么最后一位儿童分不到6盒,但至少能有3盒.则这个儿童福利院的儿童最少有________个,最多有________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交x轴于A,B两点,点P在优弧![]() 上.
上.
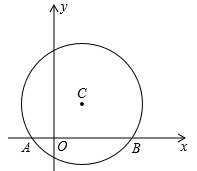
(1)求出A,B两点的坐标;
(2)试确定经过A、B且以点P为顶点的抛物线解析式;
(3)在该抛物线上是否存在一点D,使线段OP与CD互相平分?若存在,求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标;
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填入相应的集合内:+8.5,-3![]() ,0.3,0,-3.4,12,-9,4
,0.3,0,-3.4,12,-9,4![]() ,-1.2,-2.
,-1.2,-2.
(1)正数集合:{___________…};
(2)整数集合:{___________…};
(3)非正整数集合:{_____________…};
(4)负分数集合:{ ________________…}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系第一象限中,已知点A坐标为(1,0),点D坐标为(1,3),点G坐标为(1,1),动点E从点G出发,以每秒1个单位长度的速度匀速向点D方向运动,与此同时,x轴上动点B从点A出发,以相同的速度向右运动,两动点运动时间为t(0<t<2),以AD、AB分别为边作矩形ABCD,过点E作双曲线交线段BC于点F,作CD中点M,连接BE、EF、EM、FM.
(1)当t=1时,求点F的坐标.
(2)若BE平分∠AEF,则t的值为多少?
(3)若∠EMF为直角,则t的值为多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com