
【题目】如图,等边![]() 中,
中,![]() 是
是![]() 的角平分线,D为
的角平分线,D为![]() 上一点,以
上一点,以![]() 为一边且在
为一边且在![]() 下方作等边
下方作等边![]() ,连接
,连接![]() .
.

(1)求证:![]() ;
;
(2)已知![]() ,求点C到
,求点C到![]() 之间的距离.
之间的距离.
【答案】(1)证明见解析;(2)4.
【解析】
(1)由条件结合等边三角形的性质通过“边角边”可证明△ACD≌△BCE,可得AD=BE;
(2)由(1)的结论可知C到BE的距离和C到AD的距离相等,可求得C到BE的距离.
(1)证明:
∵△ABC和△CDE为等边三角形,
∴CD=CE,AC=BC,∠ACB=∠DCE=60°,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE;
(2)解:
由(1)可知△ACD≌△BCE,
∴S△ACD=S△BCE,
设C到BE的距离为h,则
![]() ADCO=
ADCO=![]() BEh,
BEh,
∴h=CO,
∵AO平分∠BAC,
∴CO=![]() BC=
BC=![]() AC=4,
AC=4,
即点C到BE的距离为4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某中学为促进课堂教学,提高教学质量,对七年级学生进行了一次“你最喜欢的课堂教学方式”的问卷调查.根据收回的问卷,学校绘制了如下图表,请你根据图表中提供的信息,解答下列问题.
编号 | 教学方式 | 最喜欢的频数 | 频率 |
1 | 教师讲,学生听 | 20 | 0.10 |
2 | 教师提出问题,学生探索思考 | ||
3 | 学生自行阅读教材,独立思考 | 30 | |
4 | 分组讨论,解决问题 | 0.25 |
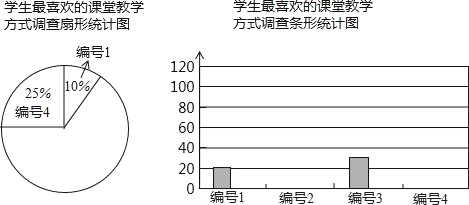
(1)收回的问卷份数为 ,把条形统计图补充完整;
(2)扇形统计图中编号1与编号4的圆心角分别是多少度?
(3)你最喜欢以上哪一种教学方式,请提出你的建议,并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是 ( )
A. 在 Rt△ABC中,若tanA=![]() ,则a=4,b=3
,则a=4,b=3
B. 在 Rt△ABC中,∠C=90°,则tanA+tanB=1
C. 在 Rt△ABC 中,∠C=90°,若a=3,b=4,则tanA=![]()
D. tan75°=tan(45°+30°)=tan45°+tan30°=1+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究活动)
如图1:已知直线a与b平行,直线c与直线a、b分别相交于点A. B,直线d与直线a、b分别相交于点C. D,点P在直线c上移动,连接PC、PD.探究∠CPD、∠PCA、∠PDB之间的数量关系.
(探究过程)
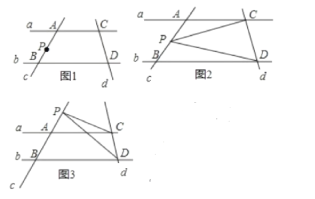
(1)当点P在点A. B之间移动时,如图2,写出∠CPD、∠PCA、∠PDB之间的关系,并说明理由.
(2)当点P在A. B两点外移动时,如图3,写出∠CPD、∠PCA、∠PDB之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高3米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有27米的距离(B,F,C在一条直线上).

(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 、
、![]() 两地相距50千米,甲于某日下午1时骑自行车从
两地相距50千米,甲于某日下午1时骑自行车从![]() 地出发驶往
地出发驶往![]() 地,乙也在同日下午骑摩托车按同路从
地,乙也在同日下午骑摩托车按同路从![]() 地出发驶往
地出发驶往![]() 地,如图所示,图中的折线
地,如图所示,图中的折线![]() 和线段
和线段![]() 分别表示甲、乙所行驶的路程
分别表示甲、乙所行驶的路程![]() (千米)与该日下午时间
(千米)与该日下午时间![]() (时)之间的关系.根据图象回答下列问题:
(时)之间的关系.根据图象回答下列问题:
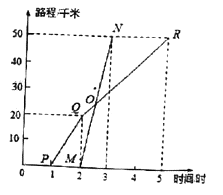
(1)甲出发___________小时后,乙才开始出发;乙的速度为__________千米/时;甲骑自行车在全程的平均速度为__________千米/时;
(2)乙出发多少小时后就追上了甲?写出解答过程;
(3)请你自己再提出一个符合题意的问题情境,并解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件,其中甲种奖品每件40元,乙种奖品每件30元.
(1)如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件;
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元,求该公司有哪几种不同的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是直线AB上的一点,OC平分∠AOB,在直线AB另一端以O为顶点作∠DOE=900。

(1) 若∠AOE=480,求∠BOD的度数。
(2) 写出图中与∠AOE互余的角。
(3) ∠AOE与∠COD有什么数量关系,请写出你的结论并说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com