
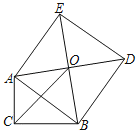
【题目】如图所示,在Rt△ABC中,∠ACB=90°,以斜边AB为边向外作正方形ABDE,且正方形的对角线交于点O,连接OC.已知AC=5![]() ,OC=12,则另一直角边BC的长为_____.(提示:分别过O向CA、CB作垂线)
,OC=12,则另一直角边BC的长为_____.(提示:分别过O向CA、CB作垂线)
【答案】7![]()
【解析】
过点O作OF⊥BC,过点A作AM⊥OF,根据正方形的性质得出∠AOB=90°,OA=OB,求出∠BOF=∠OAM,根据AAS证明△AOM≌△OBF,得出AM=OF,OM=FB,进而可得等腰三角形OCF,根据勾股定理求出CF=OF=6![]() ,求出BF,即可求出答案.
,求出BF,即可求出答案.
解:过点O作OF⊥BC于F,过点A作AM⊥OF于M,
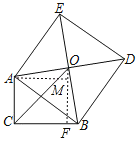
∵∠AMO=∠OFB=90°,∠ACB=∠CFM=∠AMF=90°,
∴四边形ACFM是矩形,
∴AM=CF,AC=MF=5![]() ,
,
∵四边形ABDE为正方形,
∴∠AOB=90°,OA=OB,
∴∠AOM+∠BOF=90°,
又∵∠AMO=90°,
∴∠AOM+∠OAM=90°,
∴∠BOF=∠OAM,
在△AOM和△OBF中,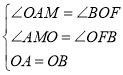 ,
,
∴△AOM≌△OBF(AAS),
∴AM=OF,OM=FB,
∴OF=CF,
∵∠CFO=90°,
∴△CFO是等腰直角三角形,
∵OC=12,
∴由勾股定理得:CF=OF=6![]() ,
,
∴BF=OM=OF﹣FM=6![]() ﹣5
﹣5![]() =
=![]() ,
,
∴BC=CF+BF=6![]() +
+![]() =7
=7![]() .
.
故答案为:7![]() .
.


科目:初中数学 来源: 题型:
【题目】课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)加工成的正方形零件的边长是多少mm?
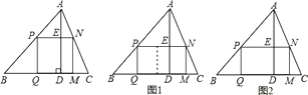
(2)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少?请你计算.
(3)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△EFC,连接AF、BE.
(1)求证:四边形ABEF是平行四边形;
(2)当∠ABC为多少度时,四边形ABEF为矩形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
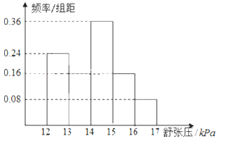
【题目】为了研究某药品的疗效,现选取若干名志愿者进行临床试验.所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组、第二组、…、第五组.如图是根据试验数据制成的频率分布直方图.
(1)若第一组接受治疗的志愿者有12人,则第三组接受治疗的志愿者有多少人?
(2)若接受治疗的志愿者共有50人,规定舒张压在14kpa以上的志愿者接受进一步的临床试验,若从三组志愿者中按比例分配20张床位,则舒张压数据在[14,15)的志愿者总共可以得到多少张床位?
查看答案和解析>>
科目:初中数学 来源: 题型:
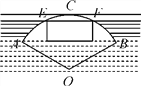
【题目】如图,一拱桥所在弧所对的圆心角为120°(即∠AOB=120°),半径为5 m,一艘6 m宽的船装载一集装箱,已知箱顶宽3.2 m,离水面AB高2 m,问此船能过桥洞吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家销售一款商品,进价每件80元,售价每件145元,每天销售40件,每销售一件需支付给商场管理费5元,未来一个月![]() 按30天计算
按30天计算![]() ,这款商品将开展“每天降价1元”的促销活动,即从第一天开始每天的单价均比前一天降低1元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件,设第x天
,这款商品将开展“每天降价1元”的促销活动,即从第一天开始每天的单价均比前一天降低1元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件,设第x天![]() 且x为整数
且x为整数![]() 的销售量为y件.
的销售量为y件.
![]() 直接写出y与x的函数关系式;
直接写出y与x的函数关系式;
![]() 设第x天的利润为w元,试求出w与x之间的函数关系式,并求出哪一天的利润最大?最大利润是多少元?
设第x天的利润为w元,试求出w与x之间的函数关系式,并求出哪一天的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业接到一批产品的生产任务,按要求必须在15天内完成.已知每件产品的售价为65元,工人甲第x天生产的产品数量为y件,y与x满足如下关系:
y=![]() .
.
(1)工人甲第几天生产的产品数量为80件?
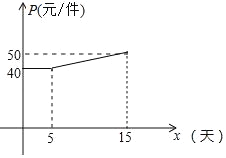
(2)设第x天(0≤x≤15)生产的产品成本为P元/件,P与x的函数图象如图,工人甲第x天创造的利润为W元.
①求P与x的函数关系式;
②求W与x的函数关系式,并求出第几天时,利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
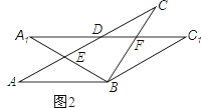
【题目】在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B顺时针旋转角α(0°<α<90°)得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.
(1)如图1,观察并猜想,在旋转过程中,线段BE与BF有怎样的数量关系?并证明你的结论;
(2)如图2,当α=30°时,试判断四边形BC1DA的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
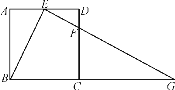
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF=![]() DC,连接EF并延长交BC的延长线于点G.
DC,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com