练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．二次函数y=mx2+（m+2）x+$\frac{1}{4}$m+2的图象与x轴只有一个交点，那么m的值为1．

    分析 根据题意得出一元二次方程的判别式△=0，得出含m的方程，解方程即可求出m的值．

    解答 解：根据题意得：y=0时，mx2+（m+2）x+$\frac{1}{4}$m+2=0，△=0，
    ∴（m+2）2-4×m（$\frac{1}{4}$m+2）=0，
    整理得：4-4m=0，
    解得：m=1．
    故答案为：1．

    点评 本题考查了抛物线与x轴的交点的性质、方程的解法；熟练掌握抛物线与x轴只有一个交点时判别式=0是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    6．在△ABC中，∠C=30°，∠A-∠B=30°，则∠A=90°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足$\frac{CF}{FD}$=$\frac{1}{3}$，连接AF并延长交⊙O于点E，连接AD、DE，若CF=2，AF=3．给出下列结论：①△ADF∽△AED；②FG=2；③tan∠E=$\frac{\sqrt{5}}{2}$；④S△DEF=4$\sqrt{5}$．其中正确的是①②④（写出所有正确结论的序号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图，已知△ABC中，∠ACB=90°，BC=6，AC=12，点D在AC上，且AD=8，将线段AD绕点A旋转至AD′，F为BD′的中点，线段CF的最大值为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，四边形ABCD为正方形．点A的坐标为（0，2），点B的坐标为（0，-3）．反比例函数y1=$\frac{k}{x}$图象经过点C，一次函数y2=ax+b的图象经过点A、C
    （1）求反比例函数与一次函数的解析式；
    （2）观察图象，在第四象限内写出使得y1＜y2成立的自变量x的取值范围；
    （3）若点P是反比例函数图象上的一点，且△OAP的面积恰好等于正方形ABCD的面积，求P点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图，矩形OABC，A（0，5），C（4，0），正比例函数y=mx（m≠0）的图象经过点B．
    （1）求正比例函数的表达式；
    （2）反比例函数$y=\frac{4}{x}（x＞0）$的图象与正比例函数的图象和边BC围成的阴影区域BNM如图所示，请直接写出阴影区域中横纵坐标都是整数的点的坐标（不包括边界）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

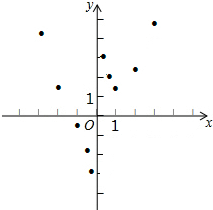    8．有这样一个问题：探究函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的图象与性质．
    小东根据学习函数的经验，对函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的图象与性质进行了探究．
    下面是小东的探究过程，请补充完整：
    （1）函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的自变量x的取值范围是x≠0；
    （2）下表是y与x的几组对应值．
     x…-3-2-1-$\frac{1}{2}$-$\frac{1}{3}$ $\frac{1}{3}$ $\frac{1}{2}$ 1 2 3…
     y… $\frac{25}{6}$ $\frac{3}{2}$-$\frac{1}{2}$-$\frac{15}{8}$-$\frac{53}{18}$$\frac{55}{18}$ $\frac{17}{8}$ $\frac{3}{2}$ $\frac{5}{2}$ m…
    求m的值；
    （3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
    （4）进一步探究发现，该函数图象在第一象限内的最低点的坐标是（1，$\frac{3}{2}$），结合函数的图象，写出该函数的其它性质（一条即可）该函数没有最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．正n边形每个内角的大小都为108°，则n=（　　）
    A．5B．6C．7D．8

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．如图，在△ABC中，AB=8，点D、E分别是BC、CA的中点，连接DE，则DE=4．

    查看答案和解析>>

    同步练习册答案