
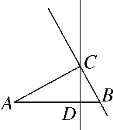
【题目】如图,在△ABC中,∠ACB=90°,AC=7cm,BC=3cm,CD为AB边上的高.点E从点B出发在直线BC上以2cm/s的速度移动,过点E作BC的垂线交直线CD于点F.当点E运动________s时,CF=AB.
【答案】5或2
【解析】
分点E在射线BC上移动和点E在射线CB上移动两种情况求解即可.
如图,当点E在射线BC上移动时,CF=AB.
∵∠A+∠ACD=90°,∠BCD+∠ACD=90°,
∴∠A=∠BCD.
又∵∠ECF=∠BCD,
∴∠A=∠ECF.
在△CFE与△ABC中, ,
,
∴△CFE≌△ABC(AAS),
∴CE=AC=7cm,
∴BE=BC+CE=10cm,10÷2=5(s).
当点E在射线CB上移动时,CF=AB.
在△CF′E′与△ABC中, ,
,
∴△CF′E′≌△ABC(AAS),
∴CE′=AC=7cm,
∴BE′=CE′-CB=4cm,4÷2=2(s).
综上可知,当点E运动5s或2s时,CF=AB.

故答案为:5或2.


科目:初中数学 来源: 题型:
【题目】(1)如图1,O是等边△ABC内一点,连接OA、OB、OC,且OA=3,OB=4,OC=5,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.求:

①旋转角的度数;
②线段OD的长;
③∠BDC的度数.
(2)如图2所示,O是等腰直角△ABC(∠ABC=90°)内一点,连接OA、OB、OC,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.当OA、OB、OC满足什么条件时,∠ODC=90°?请给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面一段文字:
问题:![]() 能化为分数形式吗?
能化为分数形式吗?
探求:步骤①设![]() ,步骤②
,步骤②![]() ,
,
步骤③![]() ,则
,则![]() ,
,
步骤④![]() ,解得:
,解得:![]() .
.
根据你对这段文字的理解,回答下列问题:
(1)步骤①到步骤②的依据是什么;
(2)仿照上述探求过程,请你尝试把![]() 化为分数形式:
化为分数形式:
(3)请你将![]() 化为分数形式,并说明理由.
化为分数形式,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有下列四种结论:①AB=AD;②∠B=∠D;③∠BAC=∠DAC;④BC=DC.以其中的2个结论作为依据不能判定△ABC≌△ADC的是( )
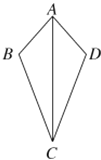
A. ①② B. ①③ C. ①④ D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O在等边△ABC内,∠AOB=100°,∠BOC=x,将△BOC绕点C顺时针旋转60°,得△ADC,连接OD.
(1)△COD的形状是 ;
(2)当x=150°时,△AOD的形状是 ;此时若OB=3,OC=5,求OA的长;
(3)当x为多少度时,△AOD为等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形的A1B1P1P2顶点P1、P2在反比例函数y= ![]() (x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,再在其右侧作正方形P2P3A2B2 , 顶点P3在反比例函数y=
(x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,再在其右侧作正方形P2P3A2B2 , 顶点P3在反比例函数y= ![]() (x>0)的图象上,顶点A2在x轴的正半轴上,则点P3的坐标为 .
(x>0)的图象上,顶点A2在x轴的正半轴上,则点P3的坐标为 . 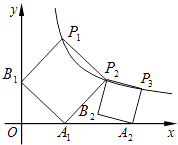
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1;(要求:A与A1,B与B1,C与C1相对应)
(2)在(1)问的结果下,连接BB1,CC1,求四边形BB1C1C的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将5张都是10元的纸币随机装入10个完全相同的信封中,设计以下几种抽奖游戏:
(1)游戏A:设计一个游戏,使任意抽取一个信封时,能抽到纸币的概率为![]() ;
;
(2)游戏B:设计一个游戏,使任意抽取一个信封时,能抽到纸币的概率为![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com