
【题目】正方形的A1B1P1P2顶点P1、P2在反比例函数y= ![]() (x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,再在其右侧作正方形P2P3A2B2 , 顶点P3在反比例函数y=
(x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,再在其右侧作正方形P2P3A2B2 , 顶点P3在反比例函数y= ![]() (x>0)的图象上,顶点A2在x轴的正半轴上,则点P3的坐标为 .
(x>0)的图象上,顶点A2在x轴的正半轴上,则点P3的坐标为 . 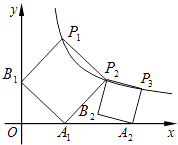
【答案】( ![]() +1,
+1, ![]() ﹣1)
﹣1)
【解析】解:作P1C⊥y轴于C,P2D⊥x轴于D,P3E⊥x轴于E,P3F⊥P2D于F,如图,
设P1(a, ![]() ),则CP1=a,OC=
),则CP1=a,OC= ![]() ,
,
∵四边形A1B1P1P2为正方形,
∴Rt△P1B1C≌Rt△B1A1O≌Rt△A1P2D,
∴OB1=P1C=A1D=a,
∴OA1=B1C=P2D= ![]() ﹣a,
﹣a,
∴OD=a+ ![]() ﹣a=
﹣a= ![]() ,
,
∴P2的坐标为( ![]() ,
, ![]() ﹣a),
﹣a),
把P2的坐标代入y= ![]() (x>0),得到(
(x>0),得到( ![]() ﹣a)
﹣a) ![]() =2,解得a=﹣1(舍)或a=1,
=2,解得a=﹣1(舍)或a=1,
∴P2(2,1),
设P3的坐标为(b, ![]() ),
),
又∵四边形P2P3A2B2为正方形,
∴Rt△P2P3F≌Rt△A2P3E,
∴P3E=P3F=DE= ![]() ,
,
∴OE=OD+DE=2+ ![]() ,
,
∴2+ ![]() =b,解得b=1﹣
=b,解得b=1﹣ ![]() (舍),b=1+
(舍),b=1+ ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ﹣1,
﹣1,
∴点P3的坐标为 ( ![]() +1,
+1, ![]() ﹣1).
﹣1).
故答案为:( ![]() +1,
+1, ![]() ﹣1).
﹣1).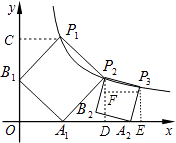
作P1C⊥y轴于C,P2D⊥x轴于D,P3E⊥x轴于E,P3F⊥P2D于F,设P1(a, ![]() ),则CP1=a,OC=
),则CP1=a,OC= ![]() ,易得Rt△P1B1C≌Rt△B1A1O≌Rt△A1P2D,则OB1=P1C=A1D=a,所以OA1=B1C=P2D=
,易得Rt△P1B1C≌Rt△B1A1O≌Rt△A1P2D,则OB1=P1C=A1D=a,所以OA1=B1C=P2D= ![]() ﹣a,则P2的坐标为(
﹣a,则P2的坐标为( ![]() ,
, ![]() ﹣a),然后把P2的坐标代入反比例函数y=
﹣a),然后把P2的坐标代入反比例函数y= ![]() ,得到a的方程,解方程求出a,得到P2的坐标;设P3的坐标为(b,
,得到a的方程,解方程求出a,得到P2的坐标;设P3的坐标为(b, ![]() ),易得Rt△P2P3F≌Rt△A2P3E,则P3E=P3F=DE=
),易得Rt△P2P3F≌Rt△A2P3E,则P3E=P3F=DE= ![]() ,通过OE=OD+DE=2+
,通过OE=OD+DE=2+ ![]() =b,这样得到关于b的方程,解方程求出b,得到P3的坐标.
=b,这样得到关于b的方程,解方程求出b,得到P3的坐标.


科目:初中数学 来源: 题型:
【题目】甲、乙两地相距210千米,一辆货车将货物由甲地运至乙地,卸载后返回甲地.若货车距乙地的距离y(千米)与时间t(时)的关系如图所示,根据所提供的信息,回答下列问题:
(1)货车在乙地卸货停留了多长时间?
(2)货车往返速度,哪个快?返回速度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】木工师傅可以用角尺测量并计算出圆的半径r,用角尺的较短边紧靠⊙O,并使较长边与⊙O相切于点C,假设角尺的较长边足够长,角尺的顶点为B,较短边AB=8cm,若读得BC长为acm,则用含a的代数式表示r为 . 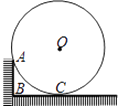
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=7cm,BC=3cm,CD为AB边上的高.点E从点B出发在直线BC上以2cm/s的速度移动,过点E作BC的垂线交直线CD于点F.当点E运动________s时,CF=AB.
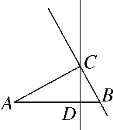
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①(﹣2)101+(﹣2)100=﹣2100;②20172+2017一定可以被2018整除;③16.9×![]() +15.1×
+15.1×![]() 能被4整除;④两个连续奇数的平方差是8的倍数.其中说法正确的个数是( )
能被4整除;④两个连续奇数的平方差是8的倍数.其中说法正确的个数是( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C、D四个车站的位置如图所示,A、B两站之间的距离AB=a﹣b,B、C两站之间的距离BC=2a﹣b,B、D两站之间的距离BD=![]() a﹣2b﹣1.求:
a﹣2b﹣1.求:
(1)A、C两站之间的距离AC;
(2)若A、C两站之间的距离AC=180km,求C、D两站之间的距离CD.
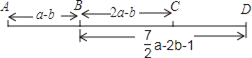
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=26°,∠C=70°,AD平分∠BAC,
AE⊥BC于点E,EF⊥AD于点F.
(1)求∠DAC的度数;
(2)求∠DEF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(3,2)、(﹣1,0),若将线段BA绕点B顺时针旋转90°得到线段BA′,则点A′的坐标为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com