
【题目】如图,直线AB∥CD,EF分别交AB、CD于G、F两点,射线FM平分∠EFD,将射线FM平移,使得端点F与点G重合且得到射线GN.若∠EFC=110°,则∠AGN的度数是( )
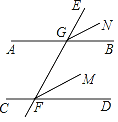
A. 120° B. 125° C. 135° D. 145°
【答案】D
【解析】
先根据邻补角的定义可求得∠EFD=70°,再根据角平分线的定义求得∠EFM=35°,由平移的性质可得GN//FM,继而可得∠EGN=∠EFM=35°,再根据AB//CD,可得∠AGE=∠EFC=110°,再由∠AGN=∠AGE+∠EGN即可得解.
∵∠EFC=110°,∠EFC+∠EFD=180°,
∴∠EFD=70°,
∵FM平分∠EFD,
∴∠EFM=35°,
∵将射线FM平移,使得端点F与点G重合且得到射线GN,
∴GN//FM,
∴∠EGN=∠EFM=35°,
∵AB//CD,
∴∠AGE=∠EFC=110°,
∴∠AGN=∠AGE+∠EGN=110°+35°=145°,
故选D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的边长为2,E为BC边的延长线上一点,CE=2,联结AE,与CD交于点F,联结BF并延长与线段DE交于点G,则BG的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+mx+n的图象经过点P(﹣3,1),对称轴是直线x=﹣1.
(1)求m,n的值;
(2)x取什么值时,y随x的增大而减小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,直径AB交弦CD于点G,CG=DG,⊙O的切线BE交DO的延长线于点E,F是DE与⊙O的交点,连接BD,BF.
(1)求证:∠CDE=∠E;
(2)若OD=4,EF=1,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE= 度;
(2)设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,则α,β之间有怎样的数量关系?请直接写出你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“综合与实践”学习活动准备制作一组三角形,记这些三角形的三边分别为a,b,c,并且这些三角形三边的长度为大于1且小于5的整数个单位长度.
(1)用记号(a,b,c)(a≤b≤c)表示一个满足条件的三角形,如(2,3,3)表示边长分别为2,3,3个单位长度的一个三角形.请列举出所有满足条件的三角形.
(2)用直尺和圆规作出三边满足a<b<c的三角形(用给定的单位长度,不写作法,保留作图痕迹).
查看答案和解析>>
科目:初中数学 来源: 题型:
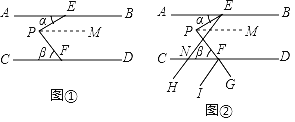
【题目】如图①,已知AB∥CD,点E、F分别是AB、CD上的点,点P是两平行线之间的一点,设∠AEP=α,∠PFC=β,在图①中,过点E作射线EH交CD于点N,作射线FI,延长PF到G,使得PE、FG分别平分∠AEH、∠DFl,得到图②.
(1)在图①中,过点P作PM∥AB,当α=20°,β=50°时,∠EPM= 度,∠EPF= 度;
(2)在(1)的条件下,求图②中∠END与∠CFI的度数;
(3)在图②中,当FI∥EH时,请直接写出α与β的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点,过点B作BE∥AD,交⊙O于点E,连接ED.
(1)求证:ED∥AC;
(2)连接AE,试证明:ABCD=AEAC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com