练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

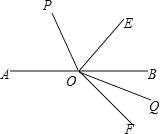
    【题目】如图，点O是直线AB上一点，∠AOE＝130°，∠EOF＝90°，OP平分∠AOE，OQ平分∠BOF，求∠POQ的度数．

    【答案】∠POQ＝135°．

    【解析】

    依据角平分线的定义即可得到∠POE的度数，再根据邻补角的定义即可得到∠BOE的度数，进而得出∠BOF 的度数，再根据角平分线的定义，即可得到∠BOQ的度数，最后依据∠POQ＝∠POE+∠BOE+∠BOQ进行计算即可．

    解：∵OP平分∠AOE，

    ∴∠POE＝∠AOE＝×130°＝65°，

    ∵∠BOE＝180°﹣∠AOE＝180°﹣130°＝50°，

    ∴∠BOF＝∠EOF﹣∠BOE＝90°﹣50°＝40°，

    ∵OQ平分∠BOF，

    ∴∠BOQ＝∠BOF＝×40°＝20°，

    ∴∠POQ＝∠POE+∠BOE+∠BOQ＝65°+50°+20°＝135°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知：如图，四边形ABCD中，对角线AC，BD相交于点O，AB=AC=AD，∠DAC=∠ABC．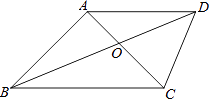
    （1）求证：BD平分∠ABC；
    （2）若∠DAC=45°，OA=1，求OC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，不添加辅助线，请写出一个能判断EB∥AC的条件：___________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司有、两种型号的客车共20辆，它们的载客量、每天的租金如下表所示.已知在20辆客车都坐满的情况下，共载客720人.

    A型号客车

    B型号客车

    载客量(人/辆)

    45

    30

    租金(元/辆)

    600

    450

    (1)求、两种型号的客车各有多少辆?

    (2)某中学计划租用、两种型号的客车共8辆，同时送七年级师生到沙家浜参加社会实践活动，已知该中学租车的总费用不超过4600元. 求最多能租用多少辆A型号客车？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

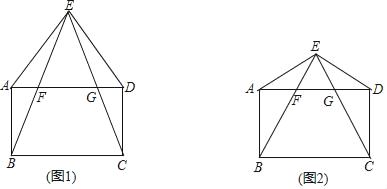
    【题目】已知：点E为矩形ABCD外一点，连接AE，DE，且AE＝DE，连接EB，EC分别与AD相交于点F，G．

    （1）如图1，求证：∠ABE＝∠DCE；

    （2）如图2，若△BCE是等边三角形，且AE＝AB，在不添加任何辅助线的情况下，请直接写出图2中四对全等的钝角三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司购买了一批A、B型芯片，其中A型芯片的单价比B型芯片的单价少9元，已知该公司用3120元购买A型芯片的条数与用4200元购买B型芯片的条数相等．

    （1）求该公司购买的A、B型芯片的单价各是多少元？

    （2）若两种芯片共购买了200条，且购买的总费用为6280元，求购买了多少条A型芯片？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠BAD＝∠CAE＝90°，AB＝AD，AE＝AC.

    (1)证明：BC=DE；

    (2)若AC＝12，求四边形ABCD的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠C=90°，AC=6，BC=8，点D、M分别在BC、AC上，Rt△BDE、Rt△EFG、Rt△GHI、Rt△IJK、Rt△KMA的斜边都在AB上，则五个小直角三角形的周长和为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，∠ABC、∠ACB的平分线相交于O，MN过点O且与BC平行．△ABC的周长为20，△AMN的周长为12，则BC的长为（ ）

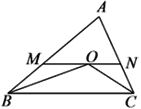
    A. 10 B. 16 C. 8 D. 4

    查看答案和解析>>

    同步练习册答案